
Окружность – это фигура на плоскости, все точки которой равноудалены от центра окружности. Окружность – самая простая фигура, которую можно провести на местности, для этого достаточно колышка для обозначения центра окружности и веревки с чертилкой. Чтобы вычертить окружность на листе бумаги, достаточно циркуля.
Хорда – это отрезок, соединяющий 2 любые точки окружности. Самой длинной хордой является диаметр, или согласно другому определению, диаметр – это хорда, проходящая через центр окружности. Нередко появляется практическая необходимость рассчитать длину хорды по известному радиусу окружности и одному из 2 углов, определяющих положение хорды (центральному или вписанному). В окружности центральный угол – это угол, вершина которого располагается в центре окружности, а вписанный угол – это угол, вершина которого лежит на окружности. Или же, вписанный угол — это угол, образованный двумя пересекающимися на окружности хордами.
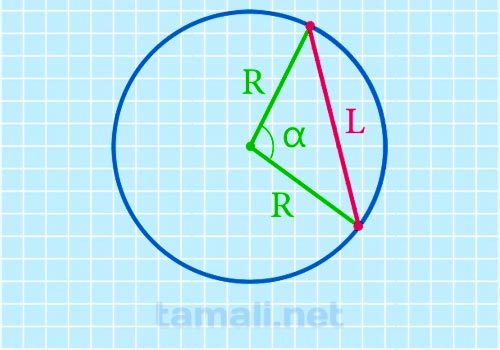
Если известен радиус и угол между радиусами, то формула будет следующая:
где R – радиус окружности, α – центральный угол между радиусами, опирающийся на хорду.
Пример. Решим практическую задачу: на местности строится из кирпича сооружение, в плане имеющее форму неполной окружности с радиусом 3 м, со стороны входа стянутой хордой, на которую опирается центральный угол в 36°. Найти длину хорды, что требуется для построения на местности без откладывания угла, а также проверки, достаточно ли в прямой стенке места для входа и устройства двери. L = 2R * sin α/2 = 2 * 3 * sin 36°/2 = 6 * 0,309 = 1,854 (м).
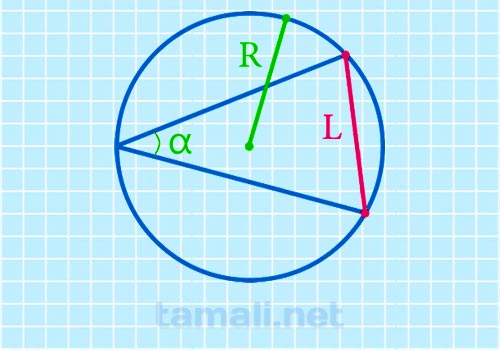
Если известен вписанный угол и радиус, то формула по нахождению длины хорды следующая:
где R — радиус, sin α — вписанный угол
Удивительно простой вид этой формулы основан на теореме о вписанном угле, согласно которой вписанный угол равен половине центрального угла, опирающегося на ту же дугу (а соответственно на ту же хорду), тем самым данная формула выводится из предыдущей.
Пример. В качестве примера, рассчитаем длину хорды в окружности радиусом 10 м, на которую опирается вписанный угол 30°. L = 2R * sin α = 2 * 10 * sin 30° = 20 * 0,5 = 10 (м). Длина хорды оказалась равной радиусу, т.е. представляет собой одну сторону вписанного в окружность шестиугольника.
Таким образом, расчет длины хорды позволяет построить на местности или бумаге любой правильный многоугольник без необходимости откладывания углов, центральных или вписанных. Уже в эпоху первобытного строя люди знали о свойствах окружности, и пользовались ими для своих целей. Одно из самых известных сооружений той поры – Стоунхендж в Англии, предположительно являвшийся астрономической обсерваторией. Следовательно, уже тогда появилась необходимость выдерживать строго центральные и вписанные углы.