
Треугольник – это форма многоугольника, которая имеет три угла, образованных тремя сторонами. Каждая из трех точек, в которых пересекаются стороны треугольника, называется его вершиной и образует определенный угол. Стороны треугольника иногда еще называют линейными длинами, а углы – угловыми. Сторону, противоположную определенному углу, обозначают той же буквой, что характеризует угол как прилегающий. Стороны обозначаются латинскими буквами a, b, c, а углы – греческими α, β, γ. Зная определенные параметры треугольника, можно найти его стороны и углы. При этом можно использовать как линейные формулы, так и обращаться к различным теоремам, например, теореме синусов и косинусов.
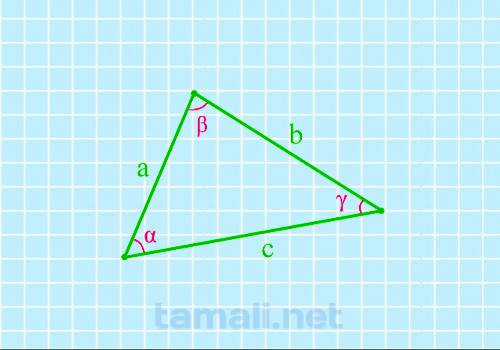
Для того, чтобы найти угол по трем сторонам, нужно вычислить косинус определенного угла. Согласно теореме косинусов, «квадрат длины стороны треугольника равен сумме квадратов двух других длин его сторон, минус удвоенное произведение этих длин сторон на косинус угла между ними». Если взять за предмет вычисления угол β, соответственно, получаем формулу: a² = b² + c² — 2 · b · c · cos (β). Из полученного равенства можно вычислить
где a, b, c — стороны треугольника.
Пример. Пусть a = 3, b = 7, c = 6. Cos (β) = (7² + 6² — 3²) : (2 · 7 · 6) = 19/21. Зная косинус, нужно воспользоваться таблицей Брадиса и по ней найти угол. По таблице Брадиса, если Cos (β) = 19/21, то β = 58,4°.
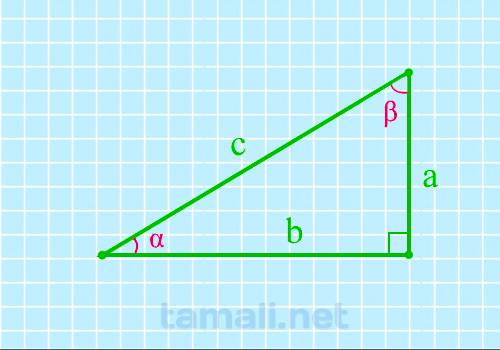
Если известен катет и гипотенуза, угол вычисляется через синус. Если известны катеты и нужно найти один из острых углов, то можно сделать это через вычисление тангенса.
где a, b — катеты, c — гипотенуза.
Пример. В прямоугольном треугольнике есть два катета a = 12, b = 9 и гипотенуза c = 15. Если известны катеты и нужно найти один из острых углов, то можно сделать это через вычисление тангенса: tg(α) = a / b, то есть tg(α) = 12 / 9. По таблице Брадиса, угол α = 53, 13°. Если известен катет и гипотенуза, угол вычисляется через синус sin(α) = a / c = 12 / 15 = 0,8. В этом случае по таблице Брадиса для синусов и косинусов, значение угла – 36, 87°.
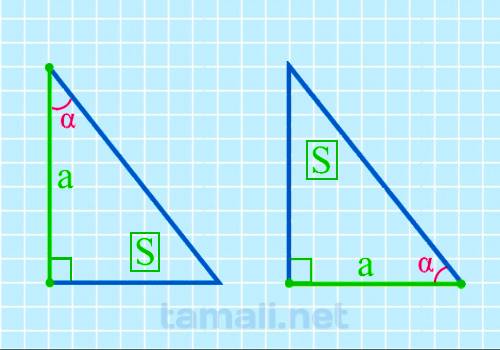
Для того, чтобы вычислить размер острого угла, нужно образовать обратную формулу от площади прямоугольного треугольника, которая вычисляется через катет и острый угол. Выглядит она следующим образом: S = (a² * tg β) / 2. Из этих показателей известный площадь S и катет a. Отсюда формула для нахождения угла будет следующая:
где a — катет, S — площадь прямоугольного треугольника.
Пример. Пусть S = 34, a = 8. Получается следующее уравнение: tg(α) = a² / 2S = 8² + 2 * 34 = 132. Таким образом выходит, что по таблице Брадиса, угол с таким тангенсом равен 43°.
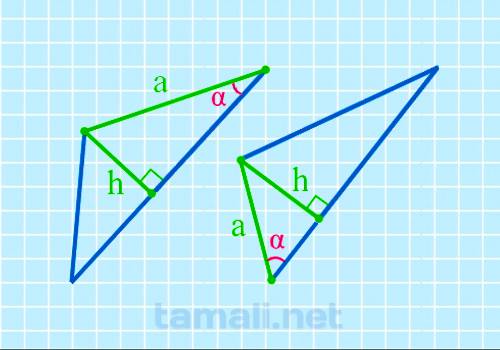
В некоторых прямоугольных треугольниках, в основании которых один острый угол, а второй 90°, один из катетов (вертикальная прямая, образующая прямой угол) называется также высотой и обозначается как h. Второй катет a остается со своим обычным названием.
где h — высота, a — катет.
Пример. Если высота h = 8, а катет a = 10, то угол α находится по формуле sin α = h / a = 8 / 10 = 0.8 то по таблице Брадиса составляет 53°
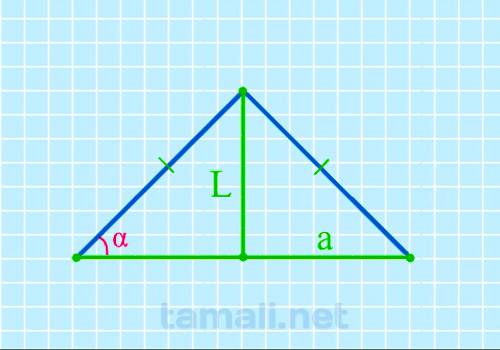
Равнобедренный треугольник ABC с основанием AC имеет биссектрису L (она же CK, делящая основание AC на два отрезка AK и KB). Также биссектриса L делит угол BCA (он же γ) пополам (каждый из этих половинок угла γ обозначается как x). То есть γ = 2х. Угол BAC (он же α) = BCA (он же γ), то есть α = γ. При этом биссектриса L (она же CK) образовала в равнобедренном треугольнике ABC новый равнобедренный треугольник AKC, в котором AK – это основание, а углы KAC и AKC равны между собой и равны значению угла γ. Учитывая то, что угол γ равен 2х (то есть двум половинкам угла), то для треугольника AKC, чтобы вычислить углы при основании, формула будет следующая:
где L — биссектриса, a — основание.
Пример. Пусть биссектриса L равна 15, основание а равно 45, подставив в формулу получим tg α = L / (a/2) = 15 / (45/2) = 33.69º
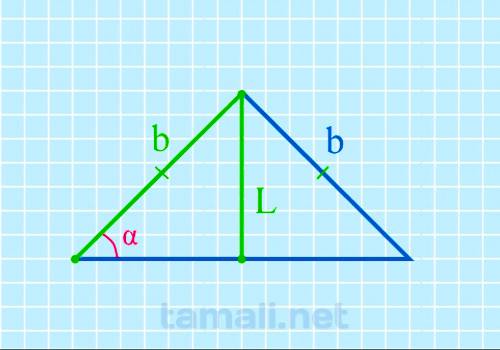
Допустим, что у равнобедренного треугольника ABC углы при основании A (α) и C (γ) равны. Также AB = BC. Биссектриса L берет начало из вершины А и пересекается с основанием АС, образуя точку пересечения K, поэтому биссектрису L также можно называть АK. L разделила угол А пополам и основание поделила на два отрезка: BK и KC. Образовался угол AKC = α (внешний угол для треугольника ABK). Согласно свойствам внешнего угла:
где L — биссектриса, b — боковая сторона.
Пример. Пусть биссектриса L равна 15, боковая сторона b равна 30, подставив в формулу получим sin α = L / b = 15/30 = 30º.
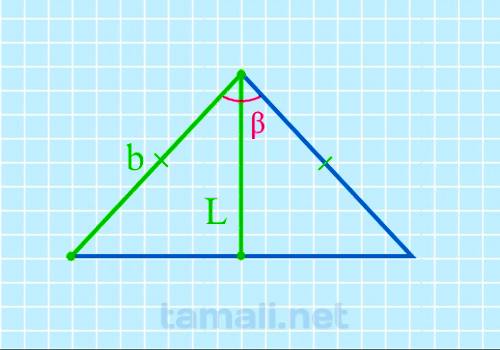
В равнобедренном треугольнике угол ABC (он же β) – это вершина треугольника. Стороны AB и BC равны, и углы у основания BAC (α) и BCA (γ) тоже равны между собой. Биссектриса L берет начало из вершины B и пересекается с основанием AC в точке K. Биссектриса BK разделила угол β пополам. Кроме того, биссектриса разделила треугольник ABC на два прямоугольных треугольника ABK и CBK, так как углы BKA и BKC – прямые и оба по 90°. Так как треугольники ABK и CBK зеркально одинаковые, для определения угла β можно взять любой из них. В свою очередь биссектриса BK разделила угол β пополам, например, на два равных угла х. Оба треугольника, образовавшихся внутри равнобедренного из-за биссектрисы, прямоугольные, поэтому, чтобы вычислить угол β (он же 2х), нужно взять за правило вычисление угла через высоту (она в данном случая является также биссектрисой) и катет (это отрезок AK или KC, которые также равны между собой, так как биссектриса и основание равнобедренного треугольника также поделила пополам).
где L — биссектриса, b — боковая сторона.
Пример. В треугольнике BKC известна биссектриса L = 47 см и боковая сторона b = 64 см. Подставив значения в формулу получим: 2cos(β) = L / b = 47 / 64 = 85.49º
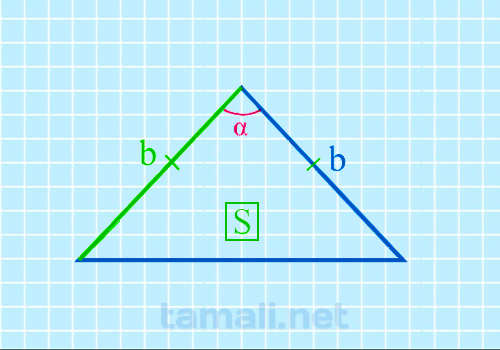
Формула площади равнобедренного треугольника S = 1/2 * bh, где b – это основание треугольника, а h – это медиана, которая разделила равнобедренный треугольника на два прямоугольных. Формула для нахождения угла между боковыми сторонами через площадь и боковую сторону будет следующая:
где b — боковая сторона равнобедренного треугольника, S — площадь.
Пример. Если площадь равна 48, а сторона 10, то угол между боковыми сторонами можно вычислить следующим образом: sin(α) = 2S / b² = 2 * 48 / 10² = 73.7º
Вне зависимости от условия задачи, известно, что сумма всех углов треугольника составляет 180°. Поэтому, элементарно вычислить один из углов можно, когда известны два других. Но для вычисления углов могут быть использованы и другие показатели. Например, для того, чтобы находить стороны и углы треугольников, в них можно проводить дополнительные меридианы, биссектрисы, чертить окружности и использовать эти фигуры как дополнительные вводные, через которые по формулам находятся неизвестные.
Углы очень удобно вычислять через синусы, косинусы, тангенсы и котангенсы, после чего сопоставлять данные с таблицей Брадиса, в которой эти величины можно сконвертировать в градусы.