
Фигура с 3 отрезками в геометрии определяется, как треугольник. Равносторонний тот, у которого все стороны имеют одинаковый размер.
Чтобы произвести измерения площади геометрической фигуры, специалисты применяют универсальную формулу, которая выглядит следующим образом: S = 1/2 * ah, где S — площадь фигуры, а — длина (чтобы узнать величину, необходимо измерить расстояние от А до В, h — высота. Для определения переменной необходимо провести медиану. Ее размер и будет высотой.
Также определить параметры равносторонней фигуры можно другими способами: через радиус и диаметр вписанной и описанной окружности, площадь описанного и вписанного круга, периметр описанной и вписанной окружности, сторону, высоту.
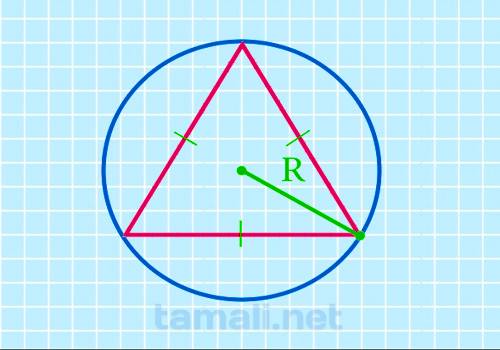
Треугольник может иметь лишь 1 описанную окружность. Для этого три отрезка геометрической фигуры должны быть внутри круга. Зная радиус, который относится, к описанной окружности, можно применить эту формулу для выполнения расчетов:
где S — площадь фигуры, R — радиус описанной окружности.
Это размеры отрезка от центра круга до любой вершины. Например, если R=5 см, то определение размеров
будет выполняться следующим образом:
S = 3√3/4*5²=3*1.732/4*25 = 32.476 м². Таким образом, применив формулу,
можно узнать искомую величину.
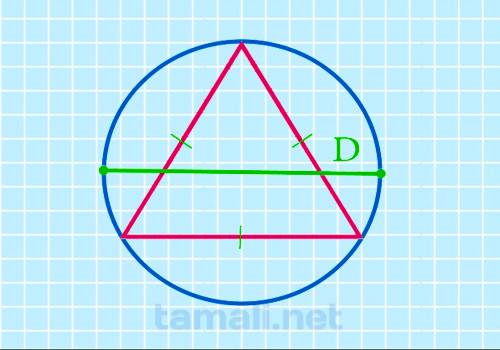
Под диаметром понимается отрезок, проходящий через центр окружности, а также соединяющий две точки. Другими словами, длина упомянутой линии и будет значением диаметра. Если значение диаметра неизвестно, но известен радиус, переменную можно рассчитать с помощью данного метода: D=2R, где R — радиус, D — диаметр. Определив диаметр описанной фигуры, можно применить такую формулу для расчетов:
где S — площадь фигуры, D — диаметр описанного круга.
То есть, длина луча, который начинается от 1 стороны круга. Также он проходит через центр окружности и описанного геометрического объекта. Завершается отрезок на противоположной части круга. К примеру, если D=6 м, то расчет размеров будет выполняться следующим образом: S = 3√3/16*6²=3*1.732/16*36 = 11.691 м² Применив эту формулу, можно найти искомую величину.
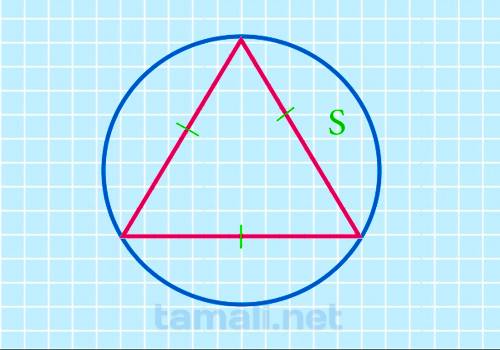
После того, как размеры круга станут известны, можно найти с помощью них площадь геометрической фигуры. Для этого необходимо воспользоваться математической формулой:
где S1 — площадь треугольника, S2 — площадь круга.
Для вычисления потребуется знать радиус окружности, чтобы с помощью него определить размеры круга. Она рассчитывается по данной формуле: S = π * R², где R — радиус, π — число Пи, значение величины всегда остается неизменным и равно 3,1415926535. На практике расчет переменной круга проще показать на конкретной задаче. Например, если R=5, π = 3,14, то следовательно S = 3,14*25 = 78,5
К примеру, если S2= 78,5, то расчет размеров будет выполняться следующим образом: S = 3 * √3 / 4π *78,5=3*1.732/4π*78,5 = 32.459 м². Используя такой метод можно определить S равностороннего объекта.
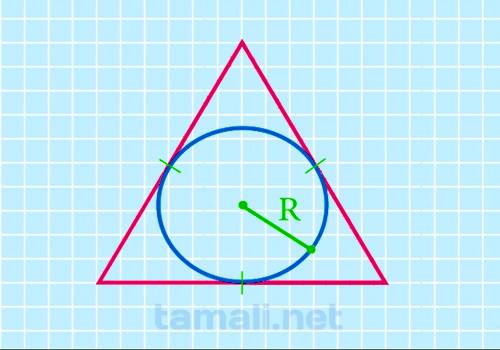
У треугольника может быть только одна вписанная окружность. Для этого круг должен быть внутри фигуры, а также соприкасаться со всеми ее сторонами. Если указан радиус, который относится, к вписанной окружности, можно использовать эту формулу для определения общих размеров искомой фигуры:
S = 3 * √3 * R² где S — площадь геометрической фигуры, R — радиус вписанного круга. Это длина прямой от центра круга до любой стороны.
К примеру, если R=5, то расчет будет осуществляться так: S = 3√3*5²=3*1.732*25 = 129.903 м². Таким образом, следуя данной формуле, можно решить задачу.
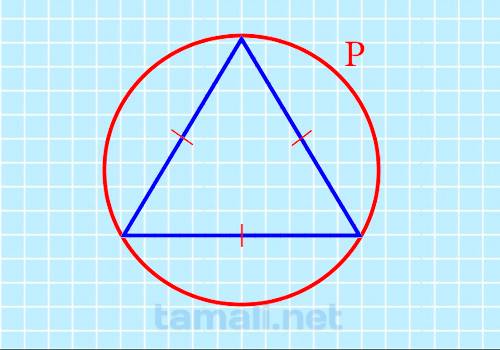
После того, как периметр круга будет подсчитан, можно определить с помощью него площадь геометрического объекта. Для этого необходимо подставить полученное значение в формулу:
S = 3√3/16π² * P² где S — площадь треугольника, P — периметр или длина круга.
Длина, а также периметр описанной окружности определяются как луч, охватывающий геометрическую фигуру в 2 измерениях. Периметр рассчитывается по такой формуле: S = 2πR где R — радиус, π — число Пи. Значение величины считается постоянным и равно 3,1415926535.
На практике расчет длины круга легче продемонстрировать на определенной задаче. Например, если R=5, π = 3,14, то следовательно Р круга = 2 * 3,14 * 5 = 31,4. К примеру, если P= 31,4, то расчет размеров будет производиться следующим образом: S = 3 * √3 / 16 π² * 31,4²=3 * 1.732 / 16 * 9,85 = 32.443 м². С помощью такой схемы можно рассчитать S искомой фигуры.
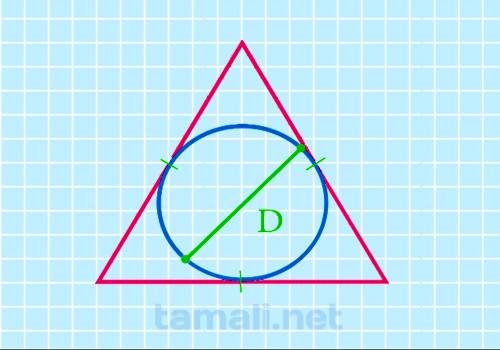
Зная диаметр вписанной окружности, рекомендуется использовать такую формулу для определения площади:
где S — площадь геометрической фигуры, D — диаметр вписанной окружности.
Диаметр в геометрии определяется, как луч, который проходит через центр окружности и соединяет две точки. Если сказать проще, то длина упомянутой линии и будет значением диаметра. В ситуации, когда известен радиус, но нет данных о диаметре, необходимо рассчитать его с помощью этой формулы: D=2R, где R — радиус, D — диаметр. То есть, длина отрезка, который начинается от стороны круга, а также пересекает центр и заканчивается на противоположной стороне.
К примеру, если D=6, то расчет размеров производится, как на представленном примере: S = 3 * √3 / 4 * 6²=3 * 1.732 / 4 * 36 = 32.475 м².
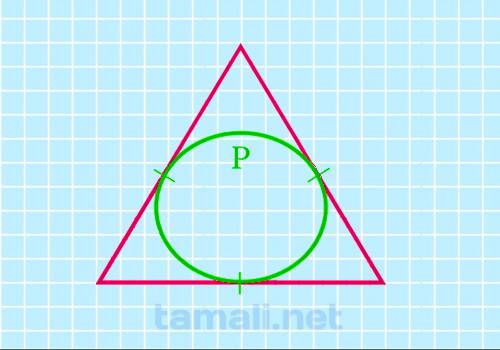
После нахождения значения периметра, можно определить с помощью него параметры требуемого объекта. Для этого потребуется подставить полученное число в формулу:
где S — площадь треугольника, P — длина вписанной окружности.
Длина или периметр окружности определяются как луч, охватывающий геометрическую фигуру в 2 измерениях. Периметр рассчитывается по формуле: S = 2πR, где R — радиус, π — число Пи. Значение величины считается постоянным и равно 3,1415926535. Чтобы было нагляднее, длину круга легче продемонстрировать на конкретной задаче. Например, если R=5, π = 3,14, то следовательно P круга = 2* 3,14*5 = 31,4.
К примеру, если P= 31,4, то расчет размеров будет производиться следующим образом: S = 3√3/4π*31,4²=3*1.732/4*3.14*985 = 407,691 м². С помощью такого способа можно рассчитать S искомой фигуры.
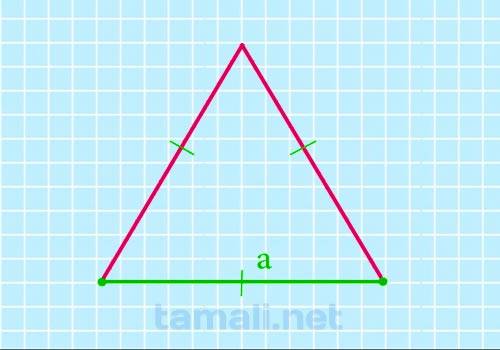
Все отрезки у этого геометрического объекта равны между собой. Поэтому, достаточно знать длину любого. Определив сторону фигуры, можно применить следующую формулу для расчета размеров:
где S — площадь геометрического объекта, a — длина отрезка.
К примеру, если a =5, то расчет размеров будет выполняться следующим образом: S = √3/4*5²=3*1.732/4*25 = 10.825 м².
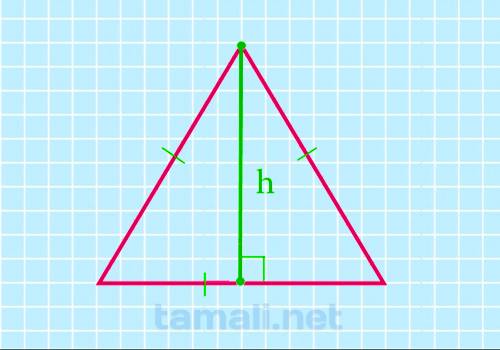
Медиана в такой фигуре является высотой и биссектрисой. По этой причине достаточно провести медиану, чтобы узнать высоту объекта. Зная высоту, можно применить следующую формулу для расчета:
где S — площадь, h — высота.
Например, если h =5, то расчет S будет осуществляться следующим способом: S = 5²/√3=25/1.732 = 14.433 м². С помощью этой формулы можно узнать общие размеры равностороннего треугольника.
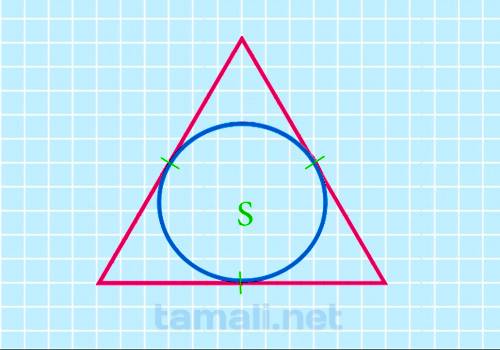
После того, как переменные круга найдены, предстоит вычислить с помощью них S фигуры. Для этого потребуется применить формулу:
где S1 — площадь треугольника, S2 — площадь вписанного круга.
Для вычисления потребуется знать радиус окружности, чтобы с помощью него определить общие размеры круга. Чтобы их рассчитать потребуется данная формула: S= π*R², где R — радиус, π — число Пи. Константа, которая всегда равна 3,1415926535. На практике расчет площади круга нагляднее продемонстрировать на конкретном упражнении. Например, если R=6, π = 3,14, то следовательно S круга = 3,14*36 = 113
К примеру, если S2= 113, то расчеты будут выглядеть следующим образом: S = 3√3/π*113=3*1.732/π*113 = 186,900 м²
Чтобы было проще понять, рекомендуется начертить на листе бумаге объект с 3 равными отрезками. У него необходимо обозначить каждую сторону латинскими буквами, например, «А» «B» «C». В результате должна получиться фигура, у которой стороны АВ=ВС=АС.
Треугольник, который имеет стороны одного размера, обладает следующими есть свойствами:
Правильно рассчитать размеры геометрической фигуры полезно не только для сдачи экзаменов, но и в повседневной жизни. Например, есть задача — оформить грядку. Для нее потребуется земля. Чтобы понимать, сколько купить материала, необходимо знать размеры участка. Если объект прямоугольной формы все просто — достаточно умножить длину на ширину. Однако, в случае с треугольниками придется использовать другую формулу.
Кроме того, необходимо понимать, какой тип фигуры представлен в задаче: равнобедренный или равносторонний.
Таким образом, понимая, как правильно вычислить S геометрической фигуры с 3 сторонами, можно легко решить задачу по геометрии или применить знания в реальной жизни.
Важно учитывать, что вышеперечисленные формулы подходят для вычисления размеров именно равностороннего треугольника. К примеру, чтобы определить площадь прямоугольного треугольника потребуется знать длину стороны «а» и «b», поскольку у них разное значение. Также необходимо измерить или найти гипотенузу прямоугольной геометрической фигуры.
Умение вычисления S геометрического объекта по формуле будет полезно при выполнении математических упражнений. Кроме того, такие знания пригодятся в реальной жизни, когда потребуется измерить размеры объекта треугольной формы. Например, при копании грядок на огороде или для проведения строительных работ по возведению здания в виде пирамиды.