
Одна из основных фигур курса математики – прямоугольник. Впервые о нем заговорили еще в Древнем Египте, а позже и в Древней Греции. Именно свойства его диагоналей помогают решить многие задания учебного курса. Подход, который сейчас используется в геометрии разработал Евклид. Формулы, представленные в данной статье, пригодятся как при решении домашних упражнений, так и на ЕГЭ. Именно такие задачки помогают набрать недостающие баллы, поэтому ими не стоит пренебрегать.
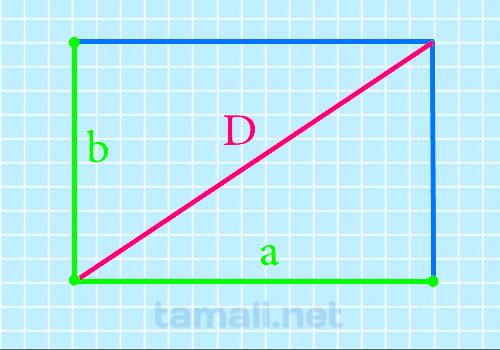
Если заданы хотя бы 2 стороны, то вычислить линию, соединяющую противоположные вершины, будет довольно просто. Применяется классическая теорема Пифагора. Достаточно подставить приведенные в дано числовые параметры в виде суммы квадратов под корнем:
Где a, b – это стороны, а d – прямая, которую мы ищем.
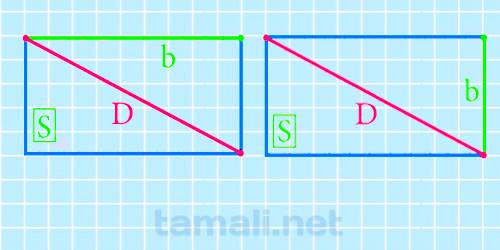
Когда в дано есть S и одна сторона, то узнать искомое значение можно используя следующее равенство:
Где D – это прямая, которую необходимо найти, a и b – любая заданная сторона, а S – площадь.
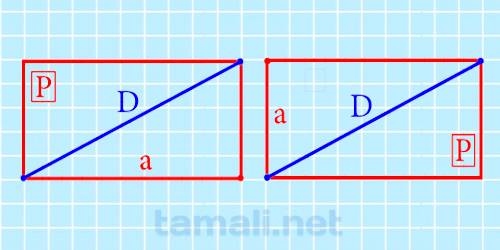
Когда задан периметр (сумма сторон) и, хотя бы одна сторона, отрезок, соединяющий несмежные точки высчитывают так:
Где P – сумма сторон, a и b – любая заданная сторона.
Рассчитать искомый отрезок можно и через соотношение сторон и площадь.
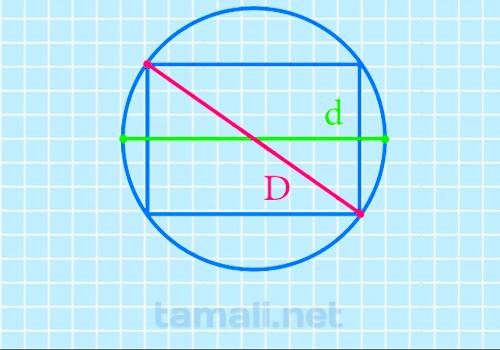
Поиск отрезка через описанную окружность еще более прост, здесь даже не придется проводить расчеты: D = d
Где d – это обозначенный диаметр.
Различить вписанную/описанную окружность легко. Когда геометрическое тело вписано куда-то, то оно всегда будет находиться в другой фигуре. Когда окружность описана, то она находится снаружи, она как бы описывает другое геометрическое тело. Описанные фигуры задевают собой точки, а вписанные – касаются сторон.
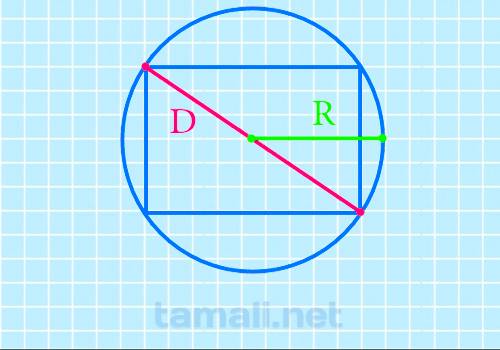
Для расчета искомого отрезка через описанную окружность нужно провести вычисления, где: D = 2R
Где R – это заданный радиус.
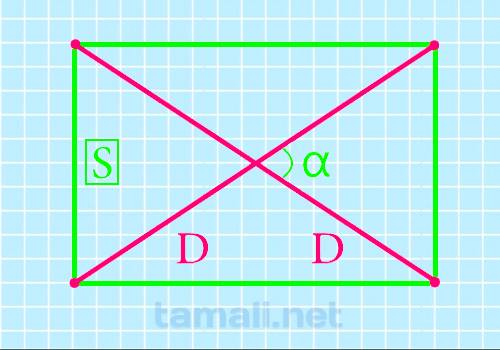
Если необходимо узнать прямую, соединяющую вершины 4-хугольника, это можно осуществить с помощью двух диагоналей. Для получения ответа к задаче понадобится sin β между ними и S (произведение длины и ширины). Расчет проводится с равенством:
Где соответственно S – это площадь, а sin β – это острый угол, расположенный внутри фигуры (меж пересекающимися прямыми).
Если в 4-хугольнике расчертить 2 отрезка, объединяющие несмежные вершины, то они будут равны меж собой (все 4 отрезка), а точка пересечения разделит их пополам.
Пересечение всегда происходит в геометрическом центре самой фигурки. Этот же центр является центром описанной окружности.
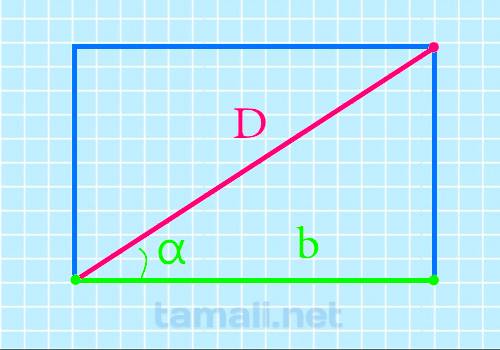
Когда одна из сторон 4-хугольника прилегает к углу, то просчитать отрезок, соединяющий вершины тоже возможно:
Где b – это сторона, прилегающая к углу, а cos a – это тот самый угол.
Косинус угла в треугольнике с прямым углом рассчитывается по формуле – длина соседней стороны, разделенная на гипотенузу. Синус – это противолежащий катет, разделенный на гипотенузу. Либо можно поступить еще проще, подсмотрев в таблицу Брадиса.
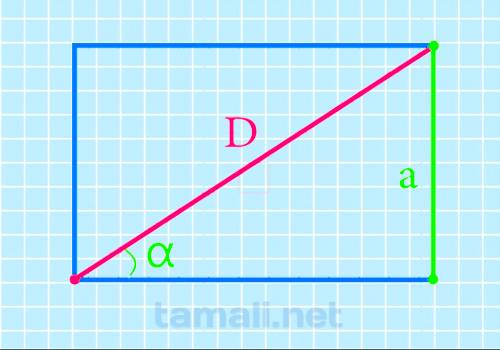
Чтобы найти нужный отрезок внутри четырехугольника, должен быть задан угол, прилегающий к искомому отрезку и сторона, противоположная углу:
Где a – это сторона четырехугольника, а sin a – это прилегающий угол.
Длинная сторона 4-хугольника– это длина, а короткая – его ширина. Помните, что каждая сторона одновременно является высотой.
Прямоугольник – это частный случай параллелограмма. Иначе 4-хугольник с попарно равными сторонами, параллельными друг другу, а также равными прямыми углами по 90⁰. Сумма углов четырехугольника составляет 360⁰.
Диагональ разделяет фигуру на два новых элемента – треугольники с прямым углом. Это прямая, объединяющая противоположные вершины. Имея 2 прямоугольных треугольника, отрезок уже можно рассчитать по теореме Пифагора. По теореме гипотенуза – это квадрат из суммы катетов (обозначенных сторон треугольника), возведенных в квадрат.
Линии, соединяющие противоположные точки в четырехугольнике всегда пересекаются друг с другом.
Отрезок обозначают как d или D. Если названы все точки, то его можно называть в соответствии с ними – AC или BD.
Знания о линии, проходящей через несмежные точки 4-хугольника может понадобиться в легких геометрических упражнениях, так и в более сложных многоуровневых задачках, которые появляются на ЕГЭ. Свойства данного отрезка помогают находить важные параметры прямоугольника. Зная данные обеих линий, соединяющих противоположные углы, можно рассчитать S геометрического тела.
Перед решением любой геометрической задачки рекомендуется сделать чертеж и обозначить всю заданную информацию. Так будет значительно проще сосредоточиться на искомом значении.
Если регулярно решать тесты по геометрии, то формулы легче запомнятся, а их применение будет доведено до автоматизма.