
Шестиугольник представляет собой геометрическую фигуру, многоугольник, который имеет шесть углов и шесть сторон.
Также существует правильный шестиугольник. Он обладает следующим свойством: все ребра и углы равны. Каждый угол составляет 120 градусов. А также он состоит из шести правильных и равных треугольников.
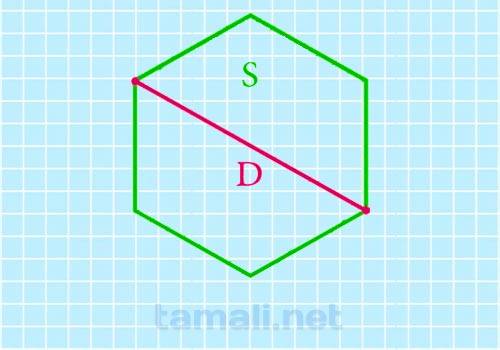
Длинной диагональю на рисунке являются отрезки ВЕ, AD и CF. Все диагонали будут равны между собой. Это свойство касается как правильной фигуры, так и неправильной. Для нахождения длинной диагонали правильного шестиугольника понадобится площадь полной фигуры (правильного шестиугольника), которую можно найти по формуле S = (a * a * √3 * 6) / 4. А диагональ находится по следующим образом:
где S — площадь правильного шестиугольника.
Пример. Сторона шестиугольника равна 6 см. Тогда площадь: S = (6 * 6 * √3 * 6) / 4 = 54√3 см. D = √((54√3 / 3√3) * 8) = 12 см.
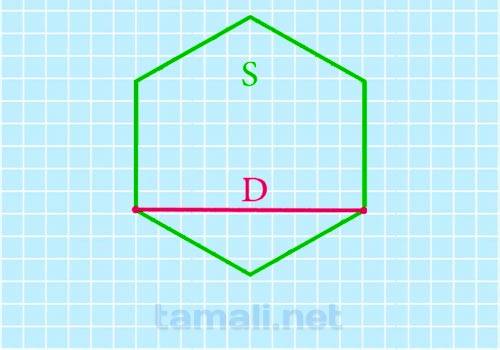
Короткими диагоналями можно назвать BD, BF, AE или же DF. Для нахождения неизвестной стороны также, как и в прошлой ситуации, понадобится площадь фигуры, которую возможно найти по следующей формуле: S = (a * a * √3 * 6) / 4. После этого найденная величина подставляется в готовую формулу:
где S — площадь правильного многоугольника.
Пример. Как и в прошлой задаче, ребро равно 6 см. Тогда площадь правильного шестиугольника = 54√3 см. Далее можно находить и искомую диагональ: D = √((54√3 / √3) * 2) = 6√3
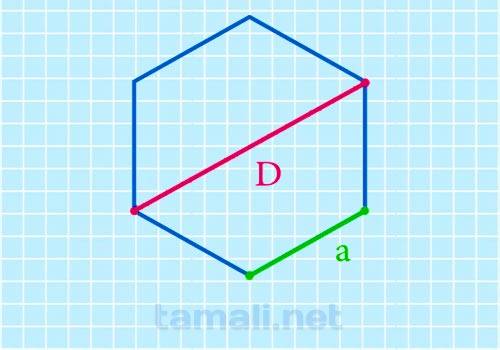
Длинной диагональю на рисунке являются отрезки ВЕ, AD и CF. Длинную диагональ правильно шестиугольника можно вычислить и без нахождения площади. Для выполнения математических действий и нахождения неизвестной переменной надо знать лишь ребро многоугольника:
где a — сторона правильного шестиугольника.
Длинная диагональ состоит из двух сторон треугольников, прилегающих друг к другу, поэтому сторону умножаем на 2.
Пример. В задаче дан правильный шестиугольник. Его ребро равно 3 см. Тогда длинная диагональ равна 6 см.
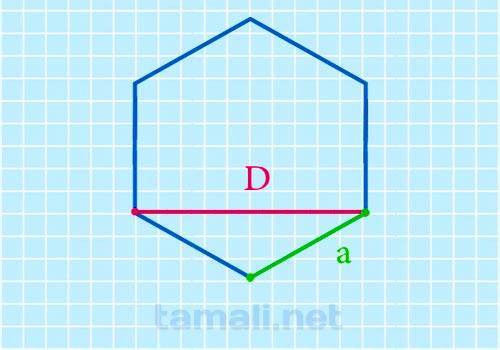
Также существует и другой способ нахождения короткой диагонали, равностороннего шестиугольника. Например, диагонали BD. Для нахождения достаточно лишь знание стороны фигуры:
где a — сторона правильного шестиугольника.
Пример. Сторона АВ равна 10 см. Тогда BD = D = √(3 * 10 * 10) = 10√3 см = 17 см.
Для более простого понимания такой темы, как вычисление диагонали правильного шестиугольника, стоит для начала увидеть, что данный многоугольник состоит из шести равносторонних и равных между собой треугольников. (Неправильный шестиугольник условно можно разделить на шесть равнобедренных треугольник). О – это центр правильного шестиугольника. Он делит диагонали на равные отрезки. Также точка пересечения длинных диагоналей является центром вписанной и описанных окружностей. Все диагонали также равны между собой и делят углы на две равные части, то есть выполняют функцию биссектрисы, а также высоты или медианы, так как были проведены в равнобедренном треугольнике. Таким образом будет легче находить какие-то неизвестные отрезки.
Однако существует и более сложный метод – через нахождение площади фигуры. Данную формулу запомнить просто: S = (a * a * √3) / 4 – она необходима, чтобы вычислить площадь равностороннего треугольника, где величина а является стороной. А вышеупомянутая фигура состоит из шести таких геометрических фигур, поэтому конечная формула будет выглядеть так: S = (a * a * √3 * 6) / 4
Таким образом, шестиугольник является не такой уж и сложной фигурой, как кажется на первый взгляд. Достаточно изучить элементарные свойства и запомнить их.