
Квадрат – это четырёхугольная плоская геометрическая фигура с равными сторонами. Квадрат считается прямоугольником, так как все его внутренние углы по 90°. Диагонали правильного четырёхугольника равны между собой, пересекаются под прямым углом и делятся точкой пересечения пополам. А также они являются биссектрисами внутренних углов (отрезок делит прямой угол на два одинаковых угла по 45°).
Знание и применение этих свойств позволяют быстро решать задачи по геометрии. Ромб с равными диагоналями, ромб с двумя соседними прямыми углами, параллелограмм с одинаковыми диагоналями, пересекающимися под прямым углом, все эти фигуры являются правильными четырёхугольниками.
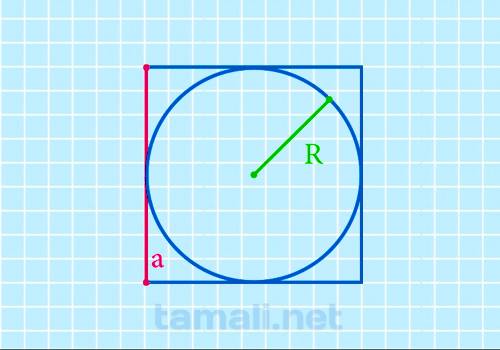
Длина стороны равна двум радиусам (диаметру) вписанной окружности:
где R — радиус.
Радиус – это расстояние от центра окружности до любой ее точки. Диаметр — отрезок, соединяющий две любые точки окружности и проходящий через центр. Радиус составляет 1/2 диаметра. Все стороны правильного четырёхугольника являются касательными прямыми к вписанной окружности. Радиус всегда перпендикулярен касательной. Вписанная окружность делит точкой касания стороны квадрата на две равные части. Зная величину диагонали, одинаковую длину стороны и диаметра легко можно объяснить благодаря теореме Пифагора: «в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». В данном случае если построить отрезки, соединяющие противоположные вершины правильного четырёхугольника, образуется равнобедренный прямоугольный треугольник, где половина стороны квадрата и радиус являются катетами, а половина диагонали — гипотенузой.
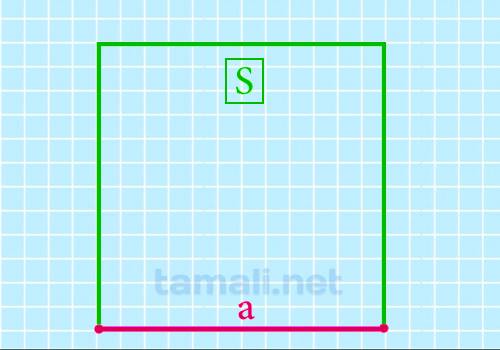
Для того чтобы определить длину стороны, зная только площадь, нужно извлечь квадратный корень из известного значения:
где S — площадь.
Это самый простой способ. Площадь плоской четырёхугольной геометрической фигуры – это числовое значение, которое характеризует размер плоскости, ограниченной четырьмя сторонами. Для нахождения площади прямоугольника необходимо умножить длину на ширину, для площади прямоугольника с равными сторонами – возвести длину в квадрат.
Также есть и другие способы для нахождения площади правильной четырёхугольной фигуры: через радиус вписанной или описанной окружности, периметр, через длину отрезка, проведенного из вершины к середине противоположной стороны. Если площадь неизвестна, но есть данные о диагонали, можно легко найти воспользоваться доступной величиной — возвести длину отрезка в квадрат и разделить на два S=d²/2.
Этот метод также опирается на теорему Пифагора. Поделив сумму квадратов катетов на два, можно найти площадь. Однако в этом случае значение не понадобится для нахождения стороны, можно быстро вычислить длину катета при помощи следующей формулы.
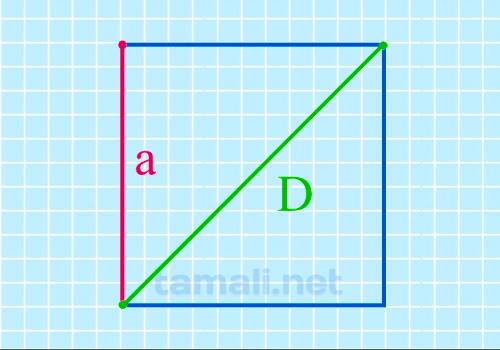
Если в задаче изначально известна длина диагонали, можно значительно сократить маршрут поиска нужной величины. На основе этого правила сторона вычисляется по формуле:
где d — диагональ.
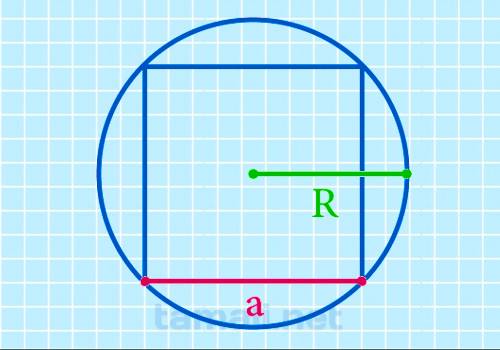
Известно, что диаметр описанной окружности равен диагонали, так как он совпадает с отрезком, соединяющим вершины двух противоположных углов, а эти вершины являются точками окружности. Формула для вычисления:
где R — радиус.
Благодаря радиусу можно найти длину диагонали, которая делит фигуру на 2 прямоугольных равнобедренных треугольника и при помощи теоремы Пифагора найти нужную величину.
Диагональ представляет собой линию, которая соединяет две вершины противоположных углов, тем самым разделяя правильный четырёхугольник на два равнобедренных прямоугольных треугольника. Найти значение таким способом не сложнее, чем через площадь. Главное, знать теорему Пифагора и уметь ею пользоваться, это самый быстрый вариант. В задачах с прямоугольными фигурами теорема часто служит выходом из сложной ситуации.
Все вычислительные способы связаны между собой. Запомнить нужные формулы несложно. Достаточно применять их на практике каждый день, частое использование одних и тех же алгоритмов приведет к автоматическому запоминаю правил. Не стоит заучивать формулы, необходимо больше рассуждать логически. Такой подход позволит решать задачи более сложного уровня и легче воспринимать любую информацию. Самым действенным методом для запоминания является практика. Отработка нескольких идентичных задач на определенное правило поможет закрепить результат на долгий срок.