
Трапеция — геометрическая фигура представляет собой выпуклый четырехугольник с параллельными противоположными сторонами. Они называются основаниями. Две другие стороны — боковые. Трапеция, у которой они одинакового размера, называется равнобедренной. Если одна из боковых сторон образует у основания угол в 90 градусов-прямоугольной.
Прямая линия, проведенная от одного основания к другому, именуется высотой трапеции. Величина ее высчитывается делением суммы оснований на 2. Диагонали — это отрезки, соединяющие противоположные углы фигуры. У равнобедренной трапеции они равны по длине. Средняя линия-прямая, делящая пополам боковые стороны.
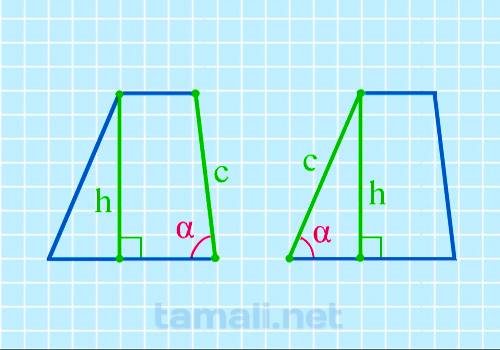
Введем обозначения: h-высота, с — боковая сторона. Угол трапеции α при основании вычисляется с помощью формулы
где: h — высота трапеции, c — боковая сторона.
Пример. Заменим буквенные обозначения условными цифрами. Пример: если высота равна 9см, боковая сторона-11см, получим: sin α = 9 / 11 = 0,818 , отсюда α = 55º. Указанное значение находим в таблице синусов. Данный показатель синуса угла соответствует величине 55 градусов.
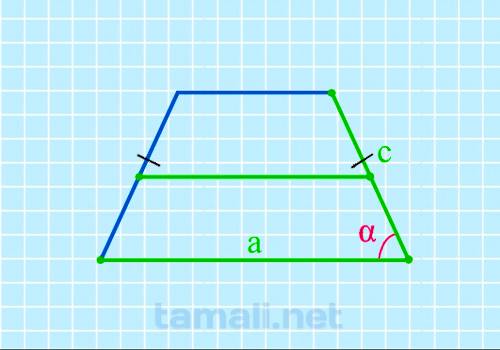
Угол равнобедренной трапеции через нижнее основание, среднюю линию и боковую сторону находится по формуле:
где а — нижнее основание, m — средняя линия, с — боковая сторона.
Пример.Заменим буквы условными цифровыми значениями. Если нижнее основание равно 8 см, средняя линия-6, а боковая сторона-4,8 см, то косинус угла равен 0,41666, что соответствует 65 градусам. cos α = (2 * 8 — 2 * 6) / 2 * 4,8 = 0, 41666, отсюда α = 65º. Равнобедренная трапеция — геометрическая фигура с нижними острыми углами. Это ее особенность.
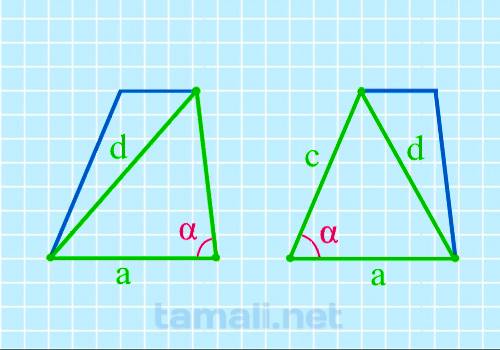
Если известны эти величины, воспользуемся формулой:
где а-нижнее основание, d-диагональ, с-боковая сторона.
Пример. При условной величине нижнего основания 4 см, диагонали — 5.7 см, боковой стороны — 4,4 см косинус равняется 0,081534, что соответствует углу 85 градусов по таблице функций. cos α= (4² + 4,4² — 5,7²) / 2*4*4,4 = 0,081534, отсюда α = 85º.
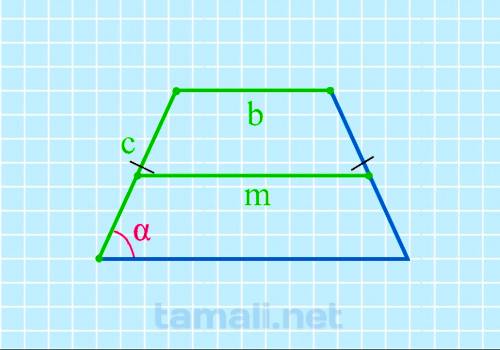
Нахождение угла равнобедренной трапеции через среднюю линию, верхнее основание и боковую сторону выполняется по предложенной формуле:
где m — средняя линия, b — верхнее основание, c — боковая сторона.
Пример. Введем условные цифровые значения. Допустим, что у равнобедренной трапеции верхнее основание равно 4 см, средняя линия-6, боковая сторона-4 см. Косинус составляет 0,5. Значение соответствует 60 градусам по таблице Брадиса. cos α = (2 * 6 — 2 * 4) / 2 * 4 = 0,5, отсюда α = 60º
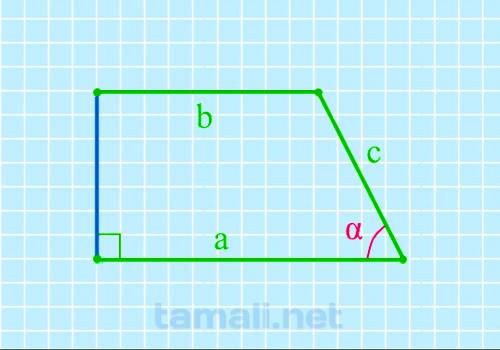
Находится по формуле
где a,b — основания, c — боковая сторона.
Пример. Если буквенные выражения заменить условными цифровыми, получится наглядный пример вычисления. Допустим, длина нижнего основания а 8 см, верхнего b-5,8 см, размер боковой стороны с-4,8. Подставив в формулу цифровые значения, получим итог: косинус равен 0,45833. Сравниваем показатель с таблицей вычисления Брадиса: он соответствует углу 63 градуса. cos α=(8 — 5,8) / 4,8 = 0,45833, отсюда α = 63º
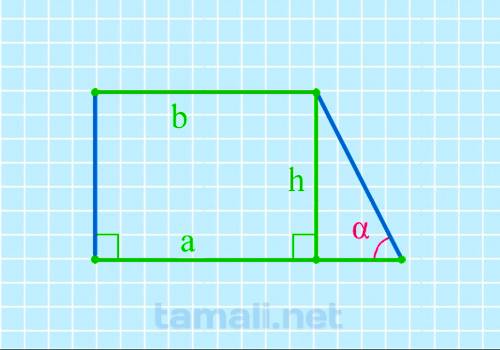
При известных указанных величинах воспользуемся следующей формулой:
где h — высота, a,b — верхнее и нижнее основания.
Пример. Введя условные цифровые значения h = 15, a = 11, b = 10 получим tg(α) = 15 / (11-10) = 15. При вычислении получим значение тангенса: 15. По таблице функций показатель соответствует 86 градусам.
Следует знать несколько закономерностей данной геометрической конструкции. У трапеции четыре угла, общая сумма которых составляет 360 градусов.
Равнобедренная отличается двумя равными острыми, прилегающими к нижнему основанию, и тупыми одинаковой величины-к верхнему. У прямоугольной трапеции два угла по 90 градусов, другие — острый и тупой. Если он прилегает к нижнему основанию, величина такого угла определяется делением высоты на разность между нижним и верхним основаниями. Угол трапеции при основании равен отношению высоты к боковой стороне.