
Окружность представляет собой замкнутую кривую, все точки которой находятся на одинаковом расстоянии от центра. Центр окружности – это точка, которая находится на равном расстоянии от всех точек, расположенных на одной прямой. Также стоит различать два понятия: окружность и круг. Круг – это просто часть некого пространства, которое ограничено окружностью. А окружностью представляет собой совокупность точек на одной прямой. Понятия связаны, но имеют существенные различия.
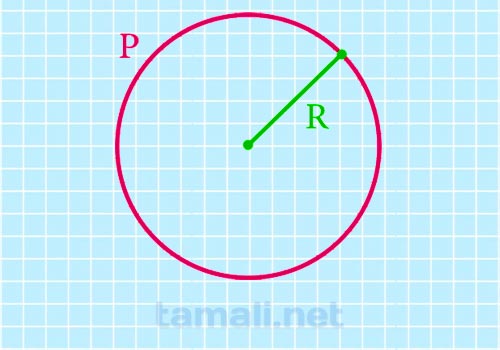
Для начала стоит сказать, что R- радиус окружности, Р – длина (периметр) окружности. Одним из самых простых способов для ее вычисления является следующий:
где R — Радиус.
Пример. Дана окружность. Учащемуся требуется найти длину окружности, когда у него есть только радиус. Радиус равен 15 см, тогда длина окружности? Решение. Находим неизвестную величину по вышеупомянутой формуле: Р = 2R * π, восполняя данные, которые были указаны в условии. К слову, π — это постоянная математическая величина. Чаще всего в ответах к заданиям она и остается в таком виде, хотя у нее есть числовое значение, которое равно 3,14. Р = 2 * 15 * 3,14 = 9 см. см. Решение не вызывает никаких вопросов, так как для нахождения неизвестной требуется только радиус окружности.
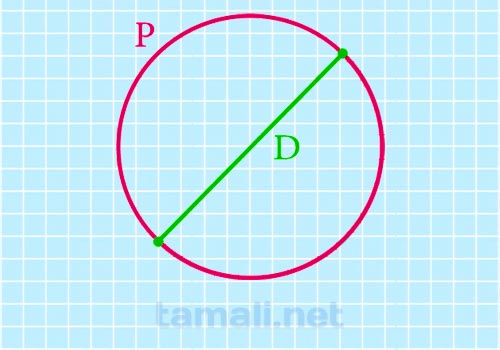
Диаметр – это радиус, который увеличили в два раза. Он тоже проходит через центр окружности и касается контура, только уже в двух местах. Но через диаметр можно найти переменную – длину (периметр) окружности. Это действие выполнимо благодаря следующей формуле:
где D – это диаметр окружности.
Пример. Учащемуся необходимо найти длину (периметр) окружности. Из известных данных только диаметр (D), который равен 20 см. Решение. Используем формулу, которая была указана выше и подставим известные данные: Р = 20 * 3,14 = 6 см.
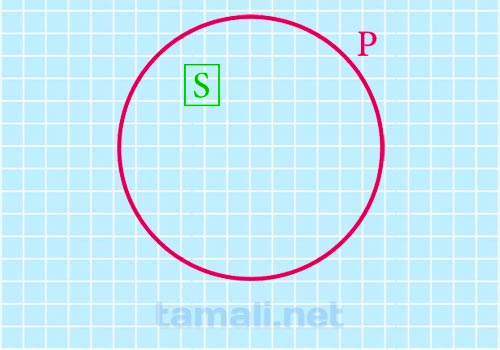
Есть еще один способ, который поможет найти длину окружности. Этот способ основан на площади окружности. Стоит упомянуть, что площадь можно найти по следующей формуле: S= πR², где S – это площадь окружности, а R – радиус окружности. А длину окружности находят следующим образом:
где S — это площадь окружности.
Пример. Дана окружность, а учащемуся требуется найти ее длину (периметр). Он имеет следующие данные: R = 3 см. Тогда чему равна длина окружности. Решение. Сначала требуется найти площадь вышеуказанной фигуры: S = πR² = 3,14 * 9 = 28,26 см. Далее можно уже находить и длину окружности, подставляя все уже известные данные в формулу, которая была упомянута выше: P = √(S * 4π) = √(28,26 * 4 * 3,14) = 1,9 см.
Каждая окружность обладает некоторыми переменными, которые можно и нужно уметь различать. Например, радиус – это расстояние от центра окружности до любой точки, которая лежит на окружности. Диаметр – это то понятие, которое связано с радиусом. Он представляет собой отрезок, который проходит через центр окружности и соединяет точки на этой же окружности, которые лежат напротив друг друга. Диаметр – это увеличенный вдвое радиус. Любая фигура имеет площадь. Окружность не является исключением. Таким образом, окружность является довольно важной фигурой, которая имеет множество составляющих, которые позволяют находить ее длину несколькими способами.