
Параллелограмм – это четырехугольник, у которого противолежащие стороны попарно параллельны. Частными случаями параллелограмма являются прямоугольник и ромб. Квадрат одновременно является частным случаем и прямоугольника и ромба, поэтому все выявленные для параллелограмма зависимости справедливы для прямоугольника, квадрата и ромба.
На практике необходимость определения угла между диагоналями на основе прочих элементов может возникнуть, в частности, при необходимости производства построений на местности и для перепроверки уже проведенных построений.
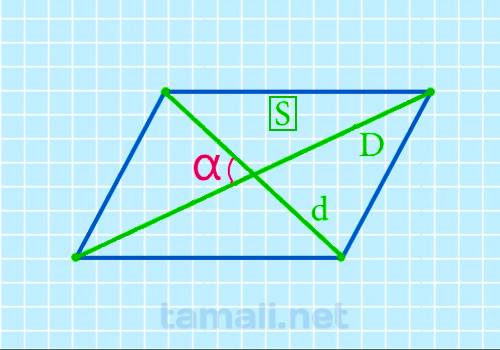
Для нахождения острого угла между диагоналями параллелограмма следует воспользоваться формулой:
где α – острый угол между диагоналями, S – площадь параллелограмма, D и d – его диагонали.
Приведем пример расчета по формуле для наглядного случая, когда диагонали перпендикулярны, и площадь данного ромба равняется половине площади прямоугольника, в который данный ромб можно вписать.
При D = 20 мм, d = 10 мм, площадь описанного прямоугольника равна 20*10=200 мм², откуда S = 200/2=100 мм².
Вычисления дают sin α = 2S/(Dd) = 2*100/(20*10) = 1, откуда α = 90°. Известный факт – диагонали ромба перпендикулярны.
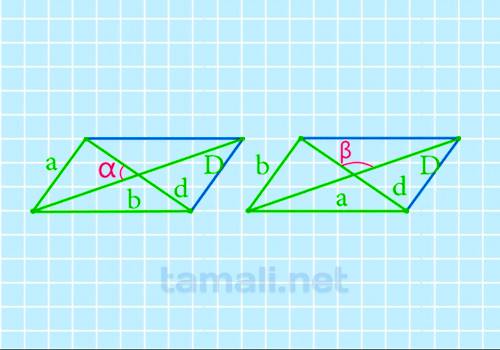
В предыдущей формуле угол определялся через диагонали и одну сторону, в данной задаче требуется определить угол по диагоналям и 2 сторонам. Тем самым, одно из условий является избыточным, и фигура по произвольным данным может не оказаться параллелограммом. Но для случая параллелограмма, т.е. взаимной увязки данных, формулы таковы:
где a и b – стороны параллелограмма, α и β – углы между диагоналями (взаимно дополнительные до 180°).
Пример приведем по предыдущему случаю, остается только рассчитать недостающую сторону b, которая из простых соображений (воспользовавшись правилом длины катета против угла в 30°) оказывается равной 20 мм. Вычисляем: cos α = (b²-a²)/(Dd) = (20²-34,64²)/(40*40) = -0,5, откуда α = 120°.
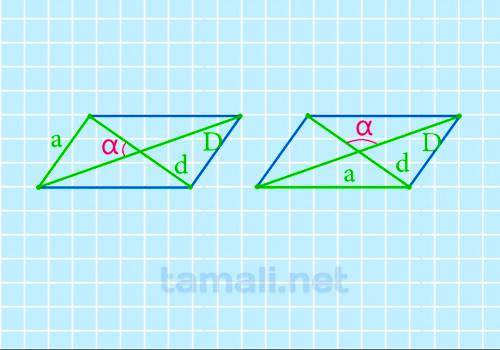
Для нахождения угла между диагоналями параллелограмма через диагонали и сторону формула такова:
где a – сторона параллелограмма, остальные обозначения прежние.
Здесь следует считаться с тем, что если в предыдущей задаче угол по условию являлся острым, в данной задаче он может быть и тупым, с отрицательным значением косинуса угла.
Пример расчета опять-таки по наглядному случаю, когда обе диагонали равны. Это прямоугольник с диагоналями D = 40 мм и d = 40 мм. При угле между диагоналями 120° половина диагонали составит 40/2 = 20 мм, половина высоты прямоугольника (она же – половина короткой стороны) составит половину от половины диагонали (в прямоугольном треугольнике противолежащий углу в 30° катет равен половине гипотенузы), т.е. 10 мм, откуда половина стороны параллелограмма составит √(20²-10²)=√300=17,32 мм, а сторона параллелограмма a = 2*17,32=34,64 мм.
Подставляем в формулу: cos α = (D² + d² – 4a²)/(2Dd) = (40²+40²-4*34,642) = ‑1600/(2*40*40) = -0,5. Значению косинуса -0,5 соответствует угол 120°. Это же значение даст и калькулятор.
Квадрат достаточно задать одним элементом – стороной. Для задания прямоугольника необходимо задать уже две его смежные стороны; для ромба сторону и угол между сторонами. Для задания же параллелограмма необходимо задание 3 его взаимно независимых элементов. Это могут быть 2 смежные стороны и угол между ними, но возможно и иное задание.
В любом четырехугольнике можно провести 2 диагонали, и они также могут входить в набор элементов для задания фигуры. В данной статье приводятся справочные формулы для определения угла между диагоналями параллелограмма через другие его элементы. Рассчитать же этот угол для каждого из 3 рассматриваемых случаев позволят калькуляторы сайта, в которые необходимо ввести известные элементы, и в результате получить синус или косинус искомого угла либо сам угол в градусах или радианах.