Площадь двухмерной фигуры – характеристика объекта, которая показывает её размер в одной плоскости. Эта величина указывается при помощи квадратных единиц.
Параллелограмм – геометрический объект, у которого противоположные края равны и параллельны. Примером может послужить прямоугольник, ромб или квадрат.
Чтобы не спутать с прямоугольником нужно знать его признаки:
- Диагонали делятся пополам точкой пересечения.
- Прилежащие углы при складывании дают 180°.
- Равенство противоположных граней.
Площадь параллелограмма, это атрибут данного объекта, который необходимо определить при помощи теорем.
Через сторону и высоту
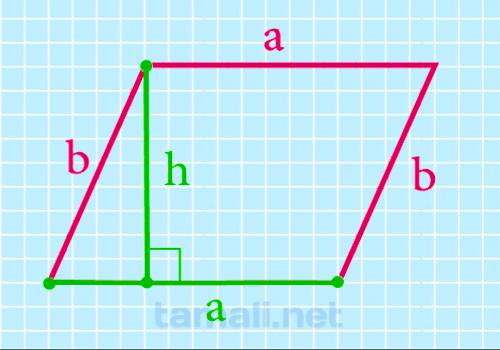
Это самая первая формула темы, которая изучается. Для неё должны быть известны высота вместе с длиной грани.
Площадь равна произведению длины стороны и высоты.
Где: a - сторона, h - высота.
Пример задания:
Дан четырёхугольник с основанием AD. Его стороны при наложении одинаковы. Основание — 15 см, высота — 12 см. Чему равен занятый участок данной фигурой?
Для начала нарисуем чертёж.
Исходя из формулы ответ будет равняться произведению 15 и 12.
S = 15 см * 12 см = 180 см2 – это будет ответ.
Через диагонали и острый угол
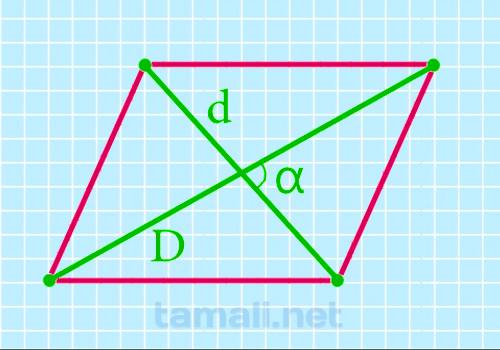
Она может пригодиться девятиклассникам в экзамене, так как недавно её добавили в задание.
Где: D, d - диагонали, sin α - острый угол между диагоналями.
Площадь будет найдена, если перемножить диагонали на синус угла при их пересечении.
Через 2 стороны и угол между ними
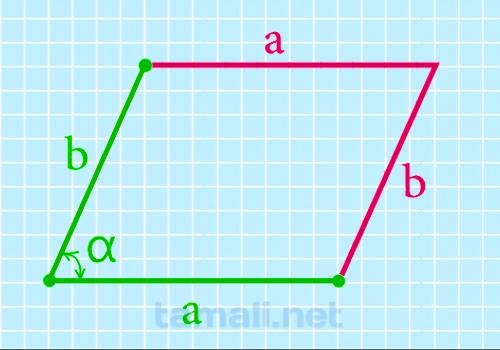
Этот способ пригодится школьникам, сдающим экзамены по математике. Эта формула изучается в 9 классе, может встретиться в ОГЭ.
Площадь можно найти, умножив 2 стороны на синус угла, который складывается из этих отрезков.
Где: a, b - стороны, sin α - угол между сторон.
Задача:
Диагонали четырёхугольника — 7 и 11. Уголок между ними равняется 45º. Узнайте величину пространства, занятой этой фигурой.
Решение:
S = 8 * 10 * sin 45º = 80 *√2/2 = 40 √2- ответ задачи.
Перейдём к примеру:
Одна из граней параллелограмма — 12, другая — 5, уголок — 45°. Определите размер участка, занятый четырёхугольником, делённый на √2.
Решение:
Зная формулу, задача будет довольно лёгкая.
S = 12 * 5 * sin 45° = 60 *√2 / 2 = 30
S/√2=30√2/√2= 30
Итак, в статье были разобраны 3 формулы по нахождению площади параллелограмма. Все они пригодятся на экзамене для 9 — 11 класса. Чтобы не тратить на лёгкие задание много времени нужно выучить эти теоремы, тогда любой тест будет простой.
