
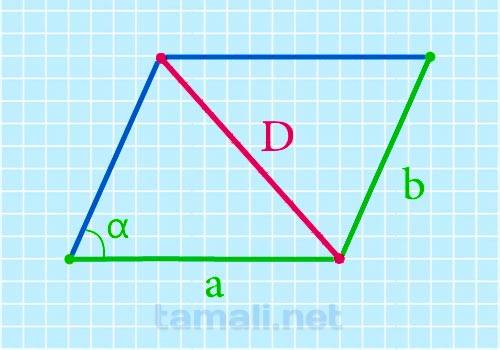
Параллелограмм представляет собой геометрическую фигуру, где лежащие напротив друг друга ребра взаимно параллельны.
В задачах по геометрии иногда нужно найти длину его диагонали. В некоторых из них это прямой вопрос, а в некоторых диагональ нужно вычислить, чтобы потом через нее вычислять другие геометрические объекты. Например, используя значения длины отрезков, соединяющих вершины, ребер этой геометрической фигуры, ее углов, вычисляется значение ее площади, другая диагональ. Если в параллелограмме неизвестны его углы, но известны стороны и угол между диагоналями, то из этих значений узнаются через расчет углы параллелограмма.
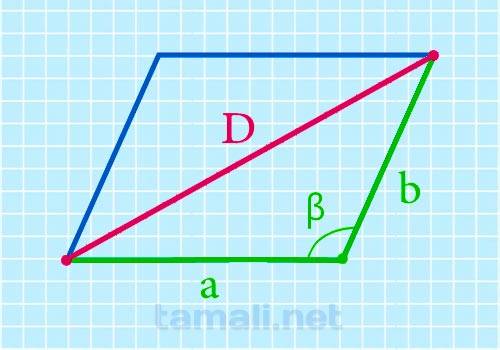
В параллелограмме для вычисления длины наибольшей диагонали при имеющихся данных о его ребрах и тупом угле между ними следует рассчитать квадрат ребер, суммировать эти значения. После этого умножить значение одного ребра на другое, на косинус тупого угла между ними, на два. Затем от первой суммы отнять это произведение и найти из этой разности квадратный корень.
где D – диагональ этой геометрической фигуры, a, b – ее ребра, cos β – косинус тупого угла между ребрами этой фигуры
Пример. Значения ребер этого четырехугольника 2 и 4, а косинус тупого угла (120 градусов) между ними -0,5. Диагональ равна: D = √(2²+ 4² – 2 * 2 * 4 * (-0,5)) = √(4+16 – 16 *( -0,5)) = √(20 + 8) = 5,3 (ответ округлен)
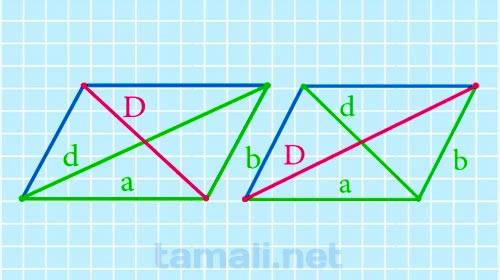
В параллелограмме для вычисления длины проведенной в нем диагонали через его стороны и другую диагональ следует возвести в квадрат каждую его сторону и умножить на 2 оба результата, затем сложить полученные значения (это первый результат). Потом следует возвести в квадрат значение длины другой диагонали (это второй результат). Затем из первого результата вычесть второй и найти из полученного значения квадратный корень.
где D – диагональ параллелограмма, a, b – его стороны, d – другая диагональ параллелограмма
Пример. Пусть стороны параллелограмма 2 и 4, а одна из диагоналей 4. Тогда вторая диагональ равна: D = √(2 * 2²+ 2 * 4² – 4²) = √(8 + 32 – 16) = √24 = 4,9 (ответ округленный)
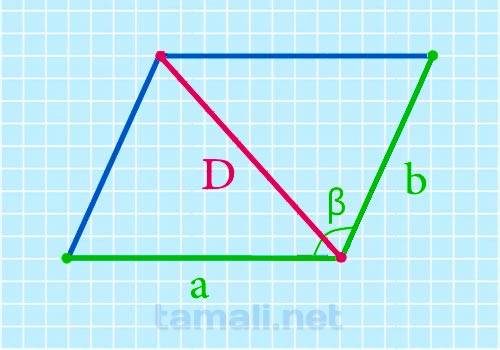
Для нахождения наименьшего отрезка соединяющего противоположные вершины в этой геометрической фигуре через его ребра и тупой угол между ними возводятся в квадрат длины его ребер, складываются полученные числа (один результат). Далее перемножаются значения длины ребер, косинус тупого угла, удваивается полученное число (это другой результат). К одному результату прибавляется другой и находится из полученного значения квадратный корень.
где D – диагональ параллелограмма, a, b – его стороны, cos β – косинус тупого угла между ребрами.
Пример. Если ребра этой геометрической фигуры 1 и 3, а косинус тупого угла (120) между ними -0,5. Тогда диагональ равна: D = √(1²+ 3² + 2 * 1 * 3 * (-0,5)) = √(1 + 9 + 6 * (-0,5)) = √(10 – 3) = 2,6 (ответ округлен)
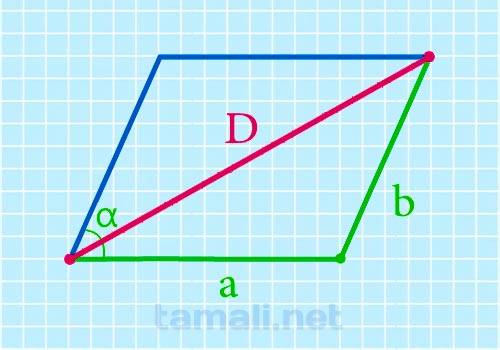
В этом четырехугольнике для расчета значения протяженности большего отрезка, соединяющего в нем расположенные друг напротив друга вершины, через два его ребра и острый угол нужно сначала возвести в квадрат значение длины его ребер, потом складываются результаты этого вычисления (это первое слагаемое для последующего сложения). Затем умножаются длины ребер друг на друга, на косинус острого угла, найденное произведение еще на 2 (это второе слагаемое). Затем оба слагаемых складываются и из суммы вычисляется квадратный корень.
где D – диагональ этой геометрической фигуры, a, b – его ребра, cos α – косинус острого угла
Пример. Если ребра этого четырехугольника 2 и 5, а косинус острого угла (60 градусов) 0,5. Тогда диагональ рассчитывается: D = √(2²+ 5² + 2 * 2 * 5 * 0,5) = √(4 + 25 + 20 * 0,5 = √(29 + 10) = 6,2 (округленно)
В параллелограмме для вычисления длины наименьшей проведенной в нем диагонали через его стороны и острый угол между ними следует возвести в квадрат каждую его сторону, затем сложить полученные значения (это первый результат). Потом следует перемножить между собой стороны, косинус тупого угла между ними, удвоить полученное значение (это второй результат). Затем из первого результата вычесть второй и найти из полученного значения квадратный корень.
где D – диагональ параллелограмма, a, b – его стороны, cos α – косинус острого угла между сторонами параллелограмма
Пример. Пусть стороны параллелограмма 2 и 4, а косинус острого угла (60) между ними 0,5. Тогда диагональ равна: D = √(2²+ 4² – 2 * 2 * 4 * 0,5) = √(4 + 16 – 16 * 0,5) = √(20 — 8) = 3,5 (ответ округлен)
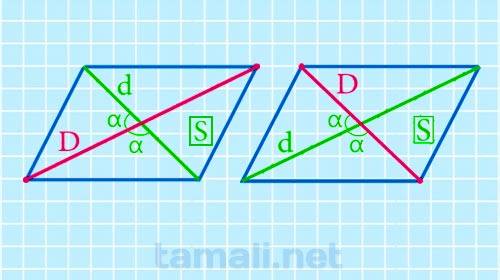
В параллелограмме для вычисления длины проведенного в нем отрезка, соединяющего противоположные вершины, используя значение его площади, другой диагонали и угол между диагоналями, следует удвоить значение его площади (это первый результат). Потом следует умножить значение длины другого отрезка, соединяющего противоположные вершины, на синус угла между диагоналями (это второй результат). Затем следует разделить первый результат на второй.
где D – диагональ параллелограмма, S – площадь параллелограмма, d – вторая диагональ этой геометрической фигуры, sinα – синус угла между диагоналями параллелограмма
Пример. Значение площади составляет 30, одна из диагоналей 4, синус угла (30 градусов) между диагоналями 0,5. Тогда другая диагональ равна: D = 2 * 30 / 4 * 0,5 = 60 / 2 = 30