
Любой многоугольник имеет периметр, который можно определить как сумму всех сторон фигуры. Для вычисления выведены формулы, опирающиеся на отдельные свойства геометрического объекта, упрощающие расчеты. Величина обозначается буквой P. Выражается в единицах измерения длины.
Под параллелограммом понимают четырехугольник, у которого противоположные стороны параллельны. Расчеты периметра фигуры основываются на следующих теоремах о свойствах данного четырехугольника:
Прямоугольник, квадрат, ромб являются частными случаями данного четырехугольника. Рассчитывая Р этих фигур, можно применить те же формулы.
Самая простая формула вычисления периметра параллелограмма учитывает то, что его противоположные стороны попарно равны. Для вычисления достаточно знать основные измерения фигуры.
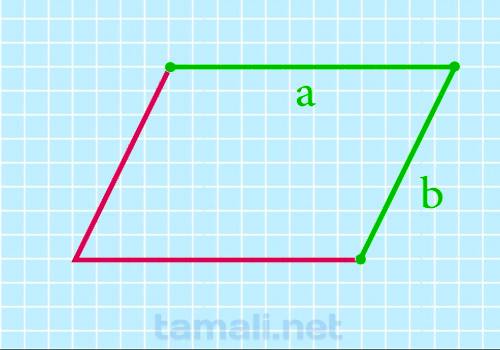
Используем общепринятые в математике обозначения: a – длина, b – ширина, P – периметр.
Тогда
формула для нахождения выглядит так:
Периметр параллелограмма равен удвоенной сумме длин его смежных сторон.
Пример 1. Требуется найти длину ограждения территории. Измерения показали, что
участок имеет следующие размеры 12 м, 11 м, 12 м, 11 м. Можно воспользоваться общим подходом:
сложить полученные величины. Но лучше применить свойство четырехугольника с попарно равными
противоположными сторонами.
P= 12 + 11 + 12 + 11 = 46 м
P = 2 * (12 + 11) = 2 * 23м
В
обоих вариантах результат расчета один – 46 м.
Пример 2. Папа с сыном мастерят фоторамку для большого настенного портрета. Они решили сделать ее в
оригинальной форме – параллелограмм с размерами 54 см и 72 см. Для расчета необходимого количества
багета нужно найти периметр рамки с припуском на угловые стыки в 5%.
P = 2∙(64+72)=2∙136=272 см
С учетом припусков умельцам потребуется 252∙1,05 =285,6 см. Багет продается только в метрах. Придется приобрести 3 м материала. Папа понимает, что остается 14 см неиспользованного материала. Зная правила расчета, мастера принимают решение увеличить каждый элемент рамки на 3 см, снизив при этом потери до 2 см.
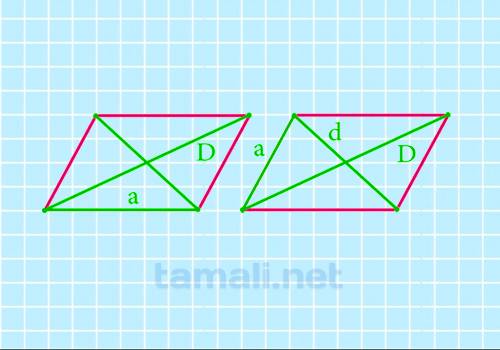
Для нахождения периметра параллелограмма через две диагонали и одну известную сторону следует воспользоваться формулой:
где D, d — диагонали, a — сторона.
Пример: Пусть D равна 12, d — 10, a = 11, все величины даны в миллиметрах. Тогда P = √(2*11² + 2*12² + 2*10² — 4*11²) = 24мм
Интересен подход, который основывается на свойствах фигуры и позволяет сделать расчеты при известных
длинах диагоналей и одной из сторон. Введем дополнительные обозначения для диагоналей – c1, c2.
Тогда математическая связь между рассматриваемыми величинами фиксируется следующим образом:
a²+b² = (c1² + c2²)/2. Из данной формулы можно найти неизвестную величину. Если
Найдя корень квадратный из полученной величины, можно воспользоваться стандартным расчетом для нахождения P. P = 2 * (a + b) Пример. Дан параллелограмм со стороной 6 см, диагоналями 8, 10 см. Требуется найти P. Квадрат ширины равен: b² = ((8² + 10²) — 6²)/2 = (64+100)/2 — 36 = 46 Вычисляя корень квадратный из 46 с точностью до десятых, получим примерно 6,8. Тогда P = 2 * (6+6,8) = 25,6 см.
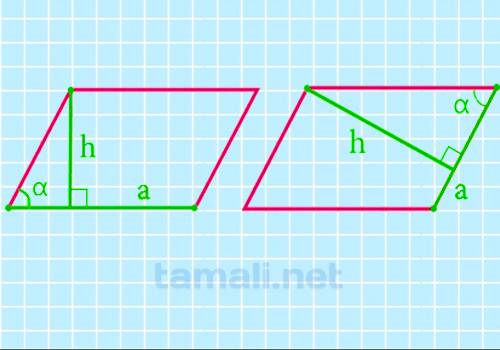
Воспользуемся известными формулами, связывающими длину известной стороны, высоту, острый угол. Обозначим:
Тогда формула для определения периметра следующая:
Пример. Для нахождения известны: сторона — 7 см, высота, проведенная к смежной стороне –
6 см, острый угол – 30º.
Вычислим ширину по заданным величинам: P = 2 * (7 + 6 / sin30) = 38см
Воспользовавшись свойствами фигуры, дополнительными преобразованиями, основанными на теореме косинусов, теореме синусов, периметр параллелограмма можно найти при различных исходных данных. В любом случае, в ходе расчетов необходимо получить значения длины и ширины, а затем подсчитать их удвоенную сумму.
К расчету периметра люди прибегают, определяя количество расходных материалов при проведении работ по ремонту, облагораживанию помещений, дачных участков, других территорий.
Умение находить сумму длин всех измерений любого четырехугольника пригодится во многих профессиях, быту. Определение количества отделочной ленты для обработки швейного изделия, плинтуса для комнаты, ограждения для участка – это те ситуации, в которых понадобятся знания по вычислению периметра любого четырехугольника.