
Ромб – геометрическая фигура, представляющая собой отдельную разновидность параллелограмма. Все имеющееся стороны равны между собой. Геометрическая фигура представляет собой отдельную разновидность параллелограмма. Все имеющееся стороны равны между собой. Чтобы исключить риски недопонимания, а также освоить принципы расчетов, рекомендуется ознакомиться с некоторыми особенностями подробней.
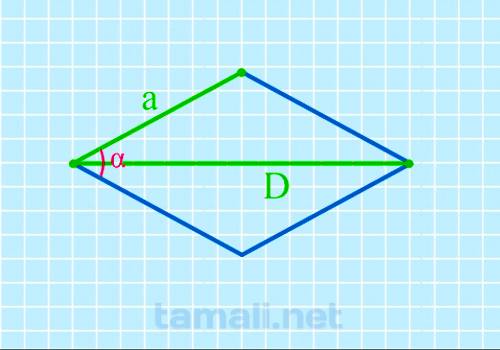
Для проведения расчетов используется формула:
где D — длинная диагональ, a — сторона.
Пример. Предположим, что длинная диагональ 25 мм, сторона – 15 мм. Отталкиваясь от полученных сведений, результат получается следующим: cos α = 25² / 2 х 15² — 1 = 67.11º
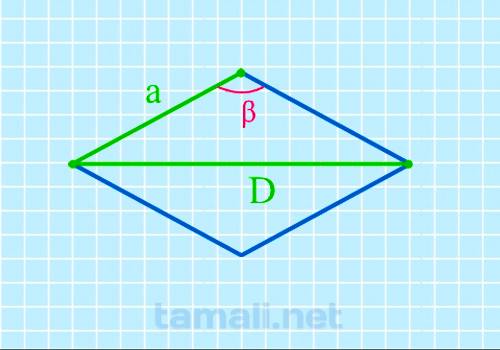
Имея достоверные данные о значение длинной диагонали (D) и стороне (a), порядок вычисления не предполагает под собой каких-либо сложностей с определением. Для этого в геометрии предлагается воспользоваться следующей формулой:
Пример. Предположим, D = 60 мм, a = 90 мм. Исходя из полученных сведений, расчет по имеющейся формуле имеет вид: cos β = 60² / 2 х 90² — 1. В таком случае cos β = 141.05. При условии, что D>a, решение не представляется возможным.
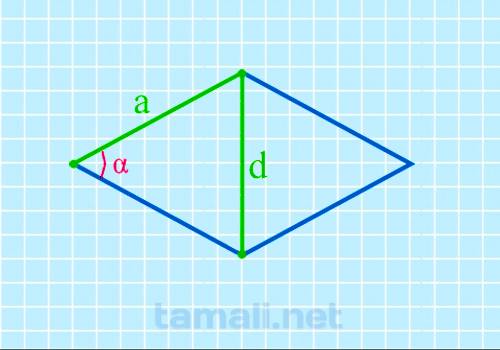
Для проведения интересующегося расчета требуется знать данные о короткой диагонали (d) и стороне (a). При условии наличия используемая формула имеет следующий вид:
где d — короткая диагональ, a — сторона.
Пример. Из представленной формулы следует, что инициировать получение интересующих данных не вызывает сложностей. Чтобы удостовериться в этом, достаточно рассмотреть пример. Допустим, что d = 40 мм, a = 25 мм. В таком случае определение результата осуществляется следующим образом: cos α = 1 – 40² / 2 х 25².
Используя калькулятор, становится известно, что cos α = 106.26. Подтвердить подлинность результата можно в режиме онлайн через специализированный сервис вычислений.
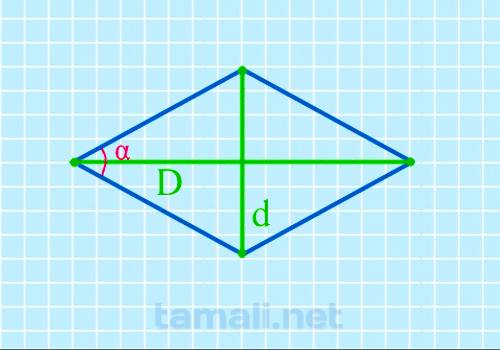
Представленный параметр расчета по праву считается одним из наиболее сложных. Чтобы исключить риски допущения ошибок и недопонимания, рекомендуется ответственно подходить к организации вычислений. Чтобы узнать информацию, чему равняется sin α, достаточно воспользоваться следующей формулой:
где D является длинной диагональю, d — короткой.
Во время определения sin α оптимальным решением станет использование стандартных математических правил. Они предполагают первичное умножение, после чего деление. Суммирование осуществляется на завершающем этапе определения значения.
Пример. Предположим, D = 85 мм, d = 15 мм. Имеющиеся значения требуется подставить в формулу. В итоге получается: sin α = (2 · 85)/85² + 15². Используя автоматизированный калькулятор для геометрии, получается, что sin α = 20.01
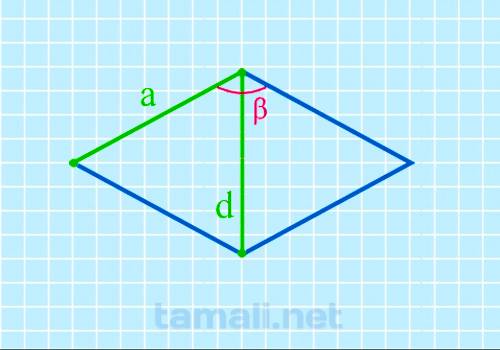
Порядок вычисления предполагает использование соответствующей формулы. Чтобы инициировать расчет требуется знать точные данные относительно короткой диагонали (d) и стороне (a). В таком случае расчет проходит следующим образом:
где d — короткая диагональ, a — сторона ромба.
Пример. Предположим, что d = 27 мм, a = 65 мм. Используя имеющуюся формулу, вычисление проходит по следующей процедуре: cos β = 1 — 27²/2х65².
Используя стандартные принципы вычисления либо специализированный онлайн калькулятор, cos β = 23.98. Чтобы гарантировать достоверность вычислений настоятельно рекомендуется выполнять проверку полученных данных несколькими способами.
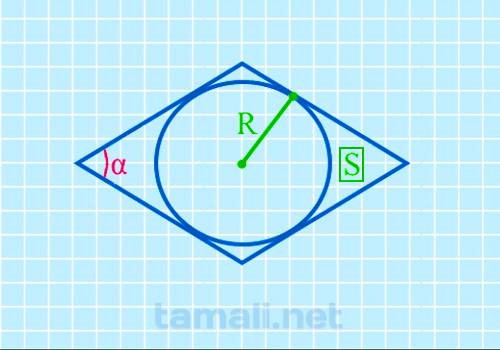
Принципы определения интересующей величины предполагают необходимость использования следующей формулы:
где R – радиус, S – заявленная площадь геометрической фигуры.
Пример. Предположим, что радиус составляет 2 см, заявленная площадь 20 мм² . Подставив имеющиеся значения в формулу, имеем следующий вид: sin(α) = 4 х 2²/20 = 53º.
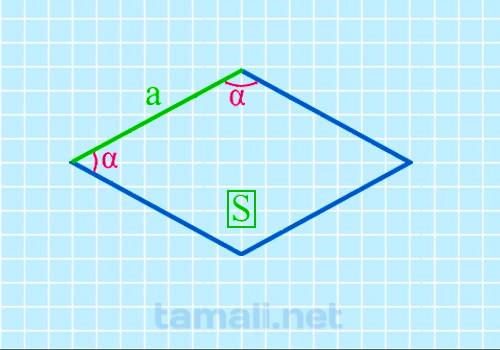
Представленный метод часто используется, чтобы узнать интересующий параметр. Главное условие – наличие известных величин из формулы, которая имеет следующий вид:
где S является площадью ромба, a — стороной.
Рассмотрим порядок определения неизвестной величины на конкретном примере. Допустим, что S = 65 мм² , a – 12 мм. В таком случае, получается: sin(α) = 65/12³ = 26,83º.
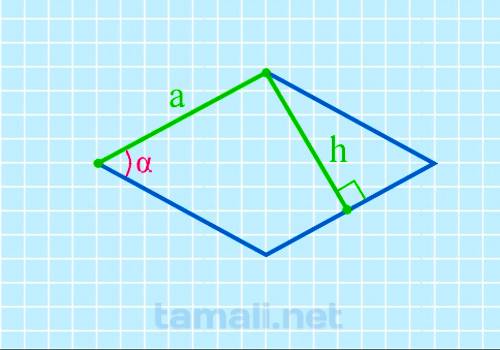
Для определения синуса предполагается использование следующей несложной формулы:
где h – заявленные показатели высоты, a — сторона.
Пример. Допустим, что высота составляет 9, сторона – 15. Следовательно, вычисления осуществляются следующим образом: sin(α) = 9/15 = 36.86 градусов.
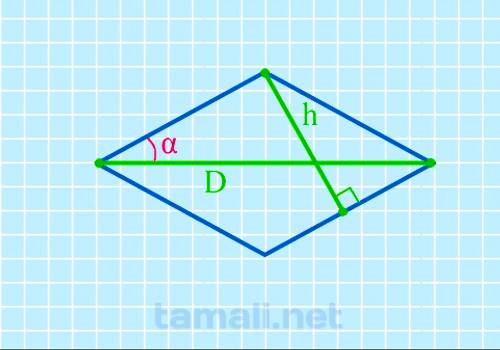
Чтобы отыскать интересующий синус, требуется воспользоваться следующим правилом определения величины:
где h – имеющаяся высота, D – заявленная длина диагонали.
Пример. Высота 43, диагональ 76. Следовательно, sin( α/2 ) = 43/76 = 34.4.
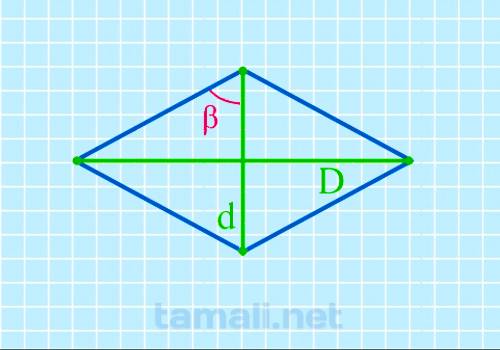
Использование рассматриваемого метода не предполагает под собой существенных сложностей. Достаточно воспользоваться специально разработанной формулой, которая имеет следующий вид:
где D выступает длинной диагональю, d — короткой.
Пример. Достаточно подставить для вычисления имеющиеся данные, чтобы в конечном итоге получить искомый результат. К примеру, D = 80 мм, d = 35 мм. Используя стандартные принципы вычисления получается: tg( β/2 ) = 80/35 = 66.37
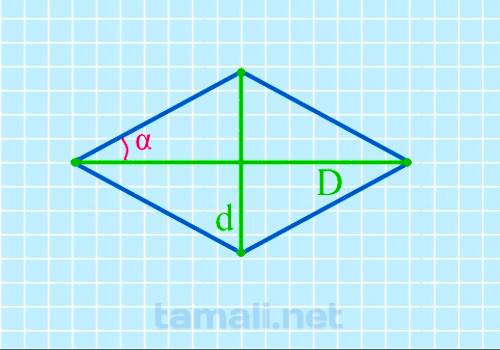
Проведение расчетов с помощью представленной методики требует наличия всех переменных, среди которых короткая и длинная диагонали. Если все необходимые параметры известны, вычисление осуществляется по представленной формуле:
где D,d – заявленная длина диагоналей.
Пример. Предположим, что D = 15 мм, d = 50 мм. Подставим имеющие значения в формулу, имеем вид: tg( α/2 ) = 50 /15 С помощью несложных подсчетов получается, что tg( α/2 ) = 73.3 градуса.
Ромб представляет собой параллелограмм, который имеем равные стороны. При наличии исключительно прямых углов – квадрат.
Дополнительно выделяют следующие признаки:
Чтобы параллелограмм считался ромбом, крайне важно соблюдение одного из нескольких условий, к которым принято относить: