Найти высоту ромба онлайн

Ромб – это фигура, являющаяся параллелограммом. Но его особенность в том, что он обладает четырьмя одинаковыми сторонами. Имеет некоторые важные геометрические свойства, а если быть точнее:

• Два угла будут равны, если они противоположные.
• Точка пересечения делить диагонали пополам.
• Стороны, которые находятся друг напротив друга, попарно равны.
• Если сложить градусную меру соседних углов, то получится 180 градусов.
• Биссектрисами ромба являются все его диагонали

Через диагонали

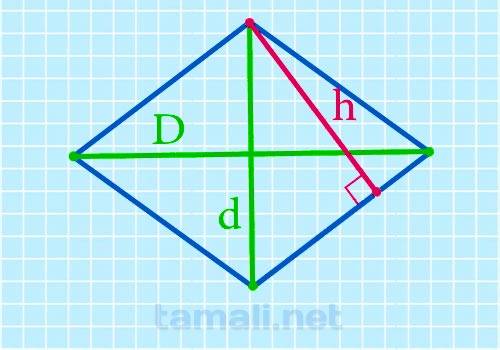
Бывают случаи, когда из всех возможных данных нам известны только две диагонали: длинная и короткая, тогда математики применяют такую формулу:

где h – высота ромба, D – длинная диагональ, d – короткая диагональ.

Пример. Имеем ромб ABCD, длинная диагональ равна 7 см, а короткая – 4 см. В условиях сказано, что нужно найти высоту, округлив ответ до десятых. Используя предыдущую формулу, подставляем вместо переменных следующие числа: h = 7 * 4 / (√7² + 4²) = 3.4. Ответ: 3.4 см.

Через диагонали и сторону

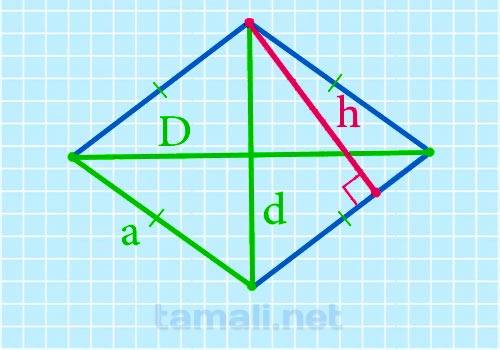
Когда в условиях задачи нам даны обе диагонали (и короткая, и длинная) вместо с одной из сторон, то нужно следовать этой формуле:

где h – высота, D – длинная диагональ, d – короткая диагональ, a – одна из сторон

Пример. Решим задачу. Дан ромб ABCD. Имеется две диагонали: короткая диагональ равна 3 см, а длинная 6. Сторона AB в длину составляет 8 см. Найдите высоту, ответ дайте в десятых. Режим задачу при помощи формулы: h = 6 * 3 / 2 * 8 = 1,2 см. Ответ: 1,2 см.

Через длинную диагональ и синус острого угла

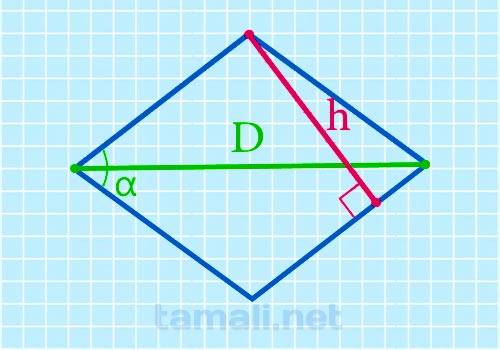
Если в задаче дан синус острого угла, а так же нам известно значение длинной диагонали, то можно использовать данный способ:

где h – высота, D – длинная диагональ, sin α – синус острого угла.

Пример. Приведём одну из возможных ситуаций. В задаче представлен ромб ABCD. Нам неизвестны его стороны, однако мы знаем, что длинная диагональ равна 9 сантиметрам. Так же мы имеем острый угол α в 30°. Нужно найти его высоту, ответ округляем до десятых. Для этого мы умножаем диагональ на sin острого угла, так как он равен 30°, то его синус равен 1/2, соответственно: h = 9 * 1/2 = 2.3 сантиметра. Ответ: 2.3 см.

Через короткую диагональ и синус тупого угла

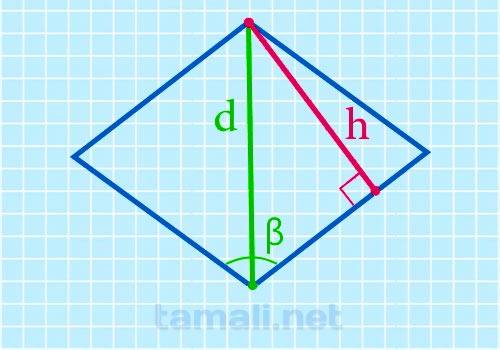
Допустим, в условиях прописано, какая длина у короткой диагонали. Так же мы знаем градус одного тупого угла. Для решения задач подобного типа используем эту формулу:

где h – высота, d – короткая диагональ, β – синус тупого угла

Пример. Решим одну из задач. Нам дан ромб ABCD. У этой фигуры короткая диагональ равна 10 см, мы знаем, что в ромбе есть тупой угол в 150°. Найдите высоту с точностью до десятых. Чтобы узнать необходимую величину, необходимо умножить D, что обозначает длинную диагональ на sin 150°/2, получается: h = 10 * (sin 150º / 2) = 9.8 сантиметров. Ответ: 9.8 см.

Через сторону и синус любого угла

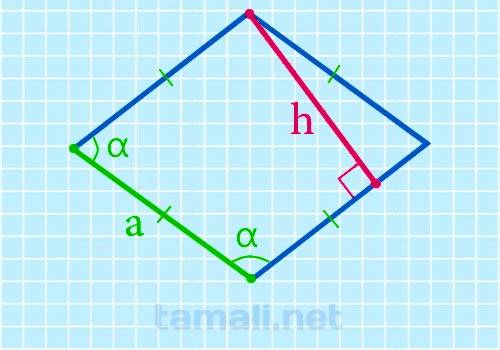
Для того чтобы найти высоту фигуры используя сторону и любой синус, нужно обратиться к следующей формуле:

где h является высотой, a – сторона ромба, sin α – синус любого угла, который мы решили взять

Пример. Рассмотрим формулу на примере. Имеем ромб ABCD, где сторона CB = 5 сантиметров, а угол C равен 90°. Чтобы найти его высоту, нам необходимо умножить CB на sin угла C. Так как синус угла 90 градусов равен 1, соответственно, получаем следующее выражение: h = 5 • 1 = 5 сантиметров составляет высота ромба ABCD. Ответ: 5 см

Если быть внимательным, то можно заметить необычные признаки ромба, по которым его легко отличить от других:

• Если в параллелограмме есть возможность вписать окружность, то это ромб.
• Если в параллелограмме все высоты равны, то это ромб.
• Если в параллелограмме под углом в 90° пересекаются диагонали, то это ромб.
• Если в параллелограмме диагонали перпендикулярны друг друга, кроме этого ещё и делятся точкой пересечения, то это ромб.
• Если все четыре стороны параллелограмма равны, то это ромб.

Задачи на нахождение различных величин ромба встречаются во многих экзаменах, в том числе на ОГЭ и ЕГЭ.

Порой в задачах необходимо определить высоту ромба, чтобы при её помощи узнать основную неизвестную величину. К примеру, для того, чтобы вычислить площадь ромба, в одной из формул нам необходимо знать высоту: , где a – это одна из сторон ромба, а h – высота. По обратной формуле можно будет найти сторону ромба, для этого будет необходимо разделить площадь на высоту: .