Найти периметр правильного шестиугольника онлайн

Правильный шестиугольник — это выпуклая многоугольная фигура с шестью сторонами одинаковой длины и углами равной величины. Другое название — гексагон. Он имеет ряд следующих особенностей и признаков:

• Длина стороны равнозначна радиусу описанной вокруг него окружности.
• Длинная диагональ представляет собой диаметр описанной окружности вокруг шестиугольника и её числовое значение — это удвоенная величина стороны.
• Короткая диагональ этой фигуры  больше его стороны в √3 раза.
• Величина каждого из шести углов имеет значение 120 градусов.
• Короткая диагональ гексагона — это перпендикуляр к одной из его сторон.
• Прямоугольный треугольник, который образуется посредством одной из сторон данной фигуры, а также его диагоналями — короткой и длинной, — имеет острые углы 30 и 60 градусов.
• Если провести 6 длинных диагоналей, то образуется 6 правильных треугольников. Все их углы будут по 60 градусов, а каждая высота равнозначна радиусу окружности, вписанной в данную фигуру.

Вариантов нахождения периметра гексагона существует множество. Например, с использованием диагоналей и площади. Ведь по условию не всегда известна длина стороны.

Через площадь

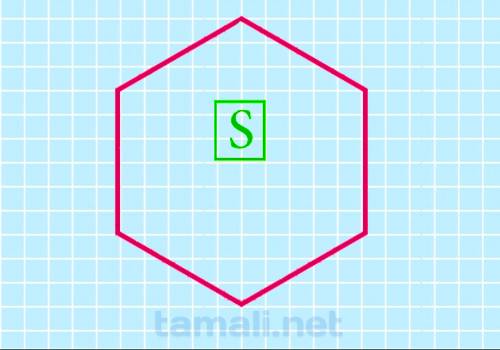
Если по условию известна только площадь, то и с этим исходным значением получится найти периметр данной фигуры. Формула используется для этого следующая: a=sqrt(2/3*S/sqrt(3)).

Вычислив значение «a», можно отыскать периметр, расчёт выглядит так:

В данной и последующих формулах sqrt — это обозначение квадратного корня.

Площадь правильного шестиугольника — это одна из основных числовых характеристик фигуры. С её помощью могут вычисляться другие параметры, значение которых нужно найти в задании.

Находится по формуле: S=(3√3*a²)/2, где S обозначается площадь правильного шестиугольника; «а» — длина его стороны.

Через короткую диагональ

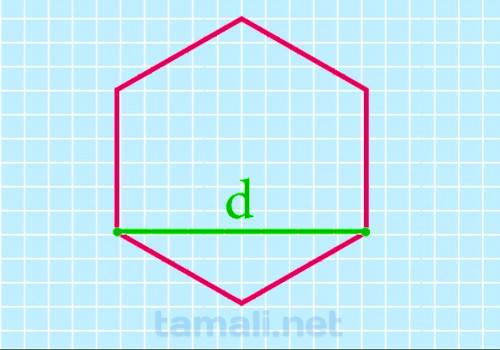
Меньшая диагональ гексагона — это величина отрезка, который соединяет одну его вершину с другой, находящейся через один угол. Она в √3 раз больше его стороны. Отрезок отсекает в шестиугольнике треугольник, который получается равнобедренным.
Для нахождения периметра в этом случае используют следующую формулу:

где d — короткая диагональ.

Через длинную диагональ

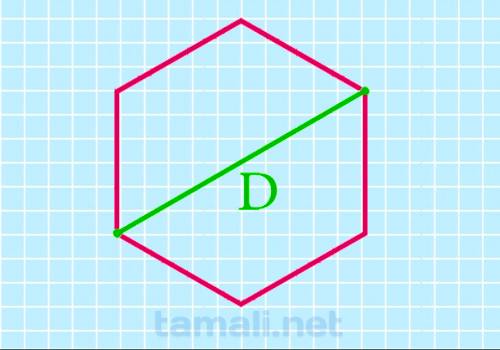
Длинная диагональ гексагона является отрезком, который проходит из одной вершины многоугольника до противоположной. Противоположная вершина находится через два угла.

Большая диагональ шестиугольника правильной формы является диаметром описанной вокруг него окружности и равна сумме двух его сторон. Соответственно, чтобы найти его периметр данным способом, нужно умножить известную величину на 3.

Через радиус описанной окружности

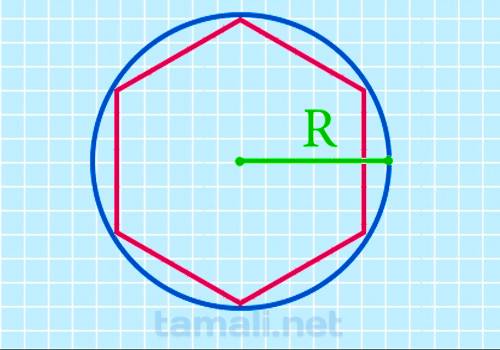
Радиус — отрезок, который идет из центра окружности к любой точке, расположенной на окружности. Радиус описанной окружности вокруг гексагона равен длине одной его стороны.
Отсюда следует, что

где r — радиус описанной окружности.
Вокруг каждой правильной геометрической фигуры можно описать окружность или вписать её внутрь. Правильный шестиугольник имеет только одну описанную окружность. Периметр равен шести радиусам этой окружности.

Через радиус вписанной окружности

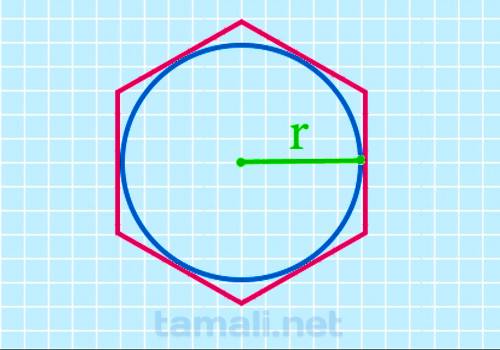
Также можно рассчитать периметр данной фигуры, если нам известен радиус вписанной в многоугольник окружности . Искомая величина равна произведению четырёх корней из трёх и радиуса вписанной окружности. Математическая формула выглядит так:

где r — радиус вписанной окружности.

Через сторону

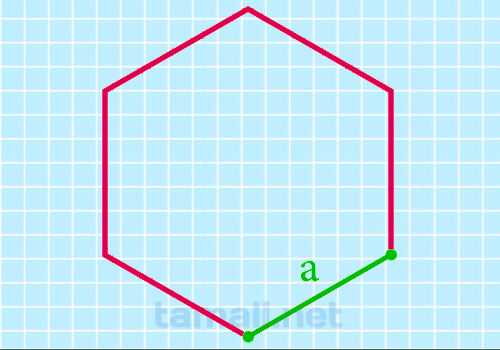
Периметр — это суммарная величина длин всех сторон плоской фигуры. Так как рассматривается шестиугольник правильной формы, требуется измерить только одну из его сторон (здесь и далее она обозначается как «а») и умножить на 6.

Данный способ очень простой, используется часто, но не является единственным. Так как значение стороны может быть неизвестно, а по условию задачи будут доступны другие исходные данные.

Найти периметр любой фигуры легко, если знать необходимые формулы и правила, а также свойства и признаки фигур. Иногда недостаточно применять только способ сложения длин всех сторон. Для этого может не хватать исходных данных по условию, поэтому используют формулы с участием иных терминов. Необходимо понимать и применять аксиомы, теоремы для решения подобных и других задач. Формулы, разобранные выше, основаны на свойствах прямоугольных треугольников. (Теорема Пифагора, синусы углов, косинусы углов и другие.)