
Квадрат – это четырёхугольник, у которого все стороны и углы раны. Он обладает следующими свойствами:
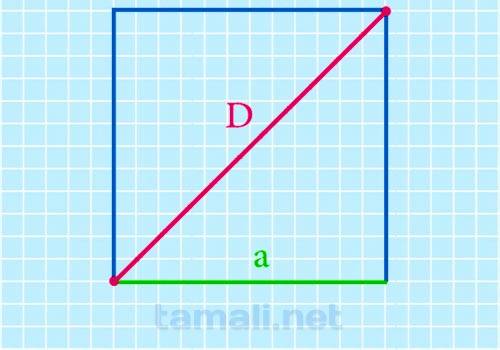
Чтобы найти диагональ квадрата через длину стороны, необходимо значение стороны а умножить на квадратный корень из двух. Данная формула выводится из теоремы Пифагора для прямоугольных треугольников, так как диагональ делит квадрат на два прямоугольных треугольника. Сама диагональ является гипотенузой данных треугольников. Теорема записывается c² = a² + b², и в данном случае вместо c выступает диагональ d, а вместо b выступает а, так как катеты равны. Преобразуем: d² = a² + a²; d² = a² * 2. Теперь необходимо извлечь квадратный корень:
где D – диагональ квадрата, а – длина стороны.
Пример. Необходимо найти диагональ квадрата d, если сторона квадрата a = 10 см. Необходимая формула: D = √(a² * 2). Вместо а подставляем значение 10: D = √(10² * 2). После того как находим квадратный корень из двух, производится умножение и получившееся значение округляем до нужного знака после запятой: D ~ 14,14 см.
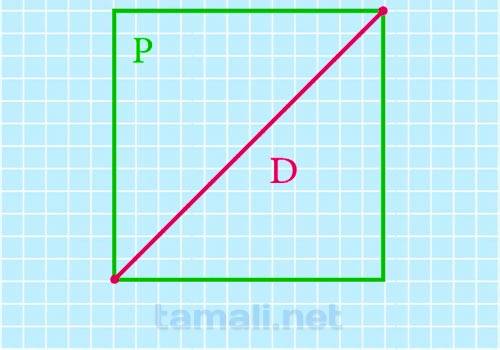
Диагональ квадрата равна отношению периметра P квадрата к произведению четырех на квадратный корень из двух.
где d – диагональ квадрата, S – периметр квадрата
Пример.Необходимо найти диагональ квадрата d, если периметр P = 20 см. Необходимая формула: D = P / 4√2. Вместо P подставляем значение 20: D = 20 / 4√2. Получившееся значение округляем до нужного знака после запятой: D ~ 3,54 см.
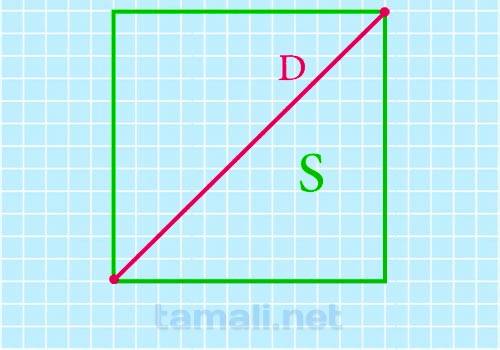
Чтобы найти диагональ квадрата через площадь S, нужно вычислить квадратный корень из произведения S × 2 . Сама площадь S для прямоугольника имеет формулу S = a * b. Так как квадрат — это прямоугольник с равными сторонами, формула для площади квадрата S = a². Если выразить сторону через площадь, формула будет иметь вид: а = √S.
где D – диагональ квадрата, S – площадь квадрата.
Пример. Необходимо найти диагональ квадрата d, если площадь S = 10 см². Необходимая формула: D = √(S * 2) Вместо S подставляем значение 10: D = √(10 * 2). Получившееся значение округляем до нужного знака после запятой: D ~ 4,47 см.
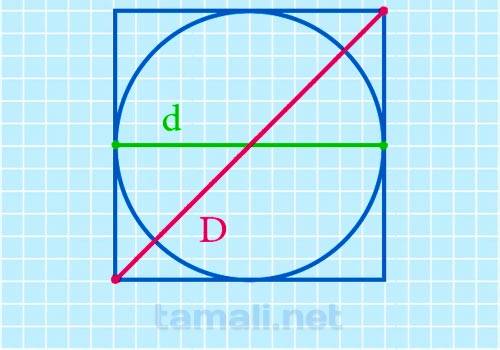
Диагональ квадрата равна произведению диаметра вписанной окружности D на квадратный корень из двух.
где D – диагональ квадрата, d – диаметр вписанной окружности.
Пример. Необходимо найти диагональ квадрата d, если диаметр вписанной окружности d = 10 см. Необходимая формула: D = d * √2. Вместо R подставляем значение 10: d = 10 * √2. Диагональ равна 14,14 см.
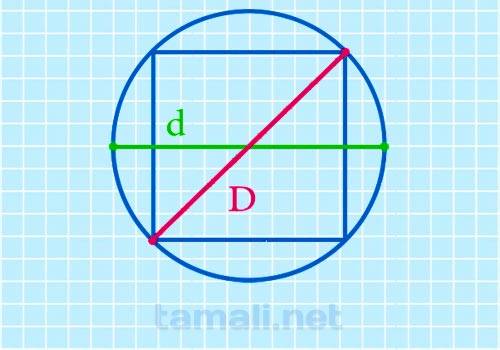
Диагональ квадрата равна диаметру d описанной окружности.
где D – диагональ квадрата, d – радиус описанной окружности.
Пример. Необходимо найти диагональ квадрата d, если диаметр описанной окружности d = 10 см. Необходимая формула: d = D. Вместо d подставляем значение 10. Диагональ равна 10 см.
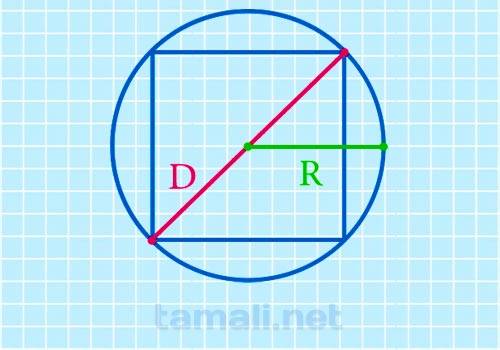
Диагональ квадрата равна радиусу описанной окружности, умноженному на два.
где D – диагональ квадрата, R – радиус описанной окружности.
Пример. Необходимо найти диагональ квадрата D, если радиус описанной окружности R = 10 см. Необходимая формула: Вместо R подставляем значение 10: D = 2 * 10. Получившееся значение округляем до нужного знака после запятой: D = 20 см.
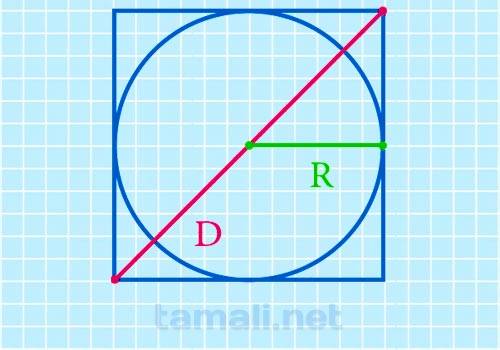
Диагональ квадрата равна произведению удвоенного радиуса вписанной окружности R на квадратный корень из двух.
где D – диагональ квадрата, R– радиус вписанной окружности.
Пример. Необходимо найти диагональ квадрата D, если радиус описанной окружности D = 10 см. Необходимая формула: D = 2R√2. Вместо R подставляем значение 10: d = 2 * 10 * √2. Диагональ равна 28,28 см.

Диагональ квадрата равна произведению квадратного корня из восьми пятых и линии C, выходящей из угла на середину стороны квадрата.
где D – диагональ квадрата, C – линия, выходящая из угла на середину квадрата.
Пример. Необходимо найти диагональ квадрата D, если линия, которая проходит из угла на середину стороны квадрата С = 10 см. Необходимая формула: D = √(8/5) * C. Вместо R подставляем значение 10: D = √(8/5) * 10. Диагональ равна 12,64 см.