
Трапецией принято называть выпуклую четырёхугольную четырехугольник с парой параллельных и двумя не параллельными сторонами. Отрезки, которые создают параллельные прямы называются «основанием трапеции», две других стороны играют роль «боковой стороны трапеции». Средняя линия трапеции будет соединять два центра боковых сторон.
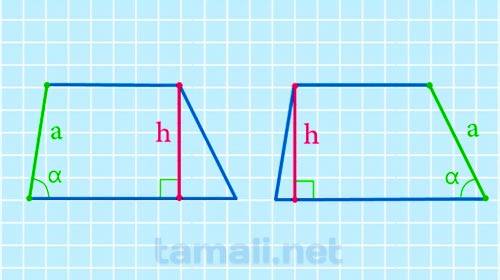
Для вычисления высоты трапеции через боковую сторону и прилегающий угол при основании нужно воспользоваться нижеприведенной формулой:
где h — это искомая высота трапеции, a — известная боковая сторона, sin α — угол при основании.
Пример. Чтобы разобраться с применением формулы, давайте рассмотрим пример. Дана некая трапеция. Нам известно, что боковая сторона равна 10 сантиметрам, а прилегающих угол составляет 30 гр. Нам нужно найти высоту данной трапеции. Для решения у нас есть вся нужная информация и формула выше. Подставляем значения в формулу: h = a · sin, h = 10 · sin 30, h = 10 · 1/2, h = 5 см
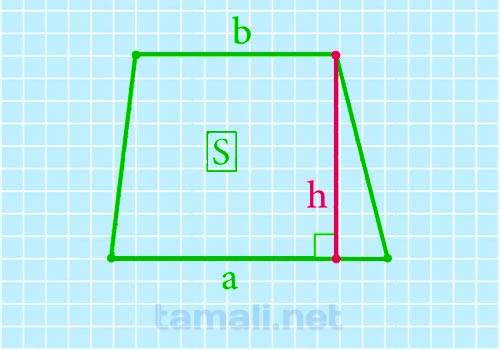
Чтобы найти высоту трапеции через известные длины основания и площадь, нужно воспользоваться формулой:
где h — это искомая высота трапеции, S — известная площадь фигуры, a и b — длины обеих оснований.
Пример. Закрепим на примере: Нам известно, что в трапеции АВСD основания a и b равны 5 и 10 сантиметров. Площадь фигуры равна 30 квадратных сантиметров. Для решения нужно воспользоваться формулой. h = (2S) / (a + b), h = (2 х 30) / (5 + 10), h = 60 /15, h = 4 см. Высота трапеции равна 4 см.
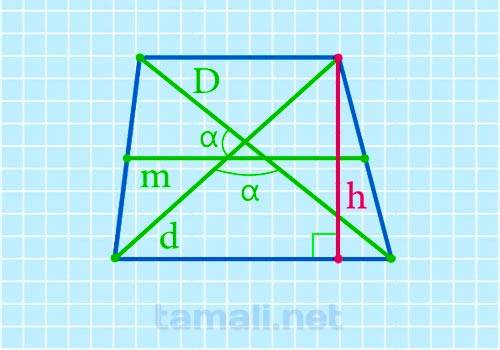
Чтобы найти высоту трапеции через среднюю линию, известные диагонали и угол между ними, нужно прибегнуть к применению выведенной формулы:
где h — это искомая высота трапеции, D и d — известные диагонали, m — средняя линия, sin(α) — угол между диагоналями.
Пример. Закрепим на примере: Дана трапеция с диагоналями 5 и 12 сантиметров. Известно, что средняя линия фигуры равна 6 см, а угол между диагоналями – 30 градусов. Применив формулу выше, мы сможем с легкостью найти высоту трапеции. h = ((D x d) / (2m)) x sin (α), h = ((5 x 12) / (2 х 6)) x sin (30), h = (60 /12) x 0.5, h = 2.5 см. Высота трапеции равна 2.5 см.
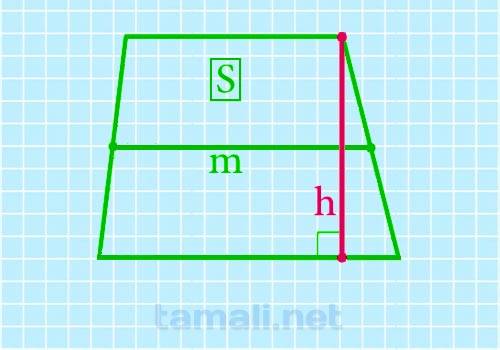
Чтобы найти высоту трапеции через площадь и среднюю линию воспользуемся выведенной формулой:
где h — это искомая высота трапеции, S — известная площадь фигуры, а m — средняя линия.
Пример. Закрепим на примере: Площадь произвольной трапеции составляет 30 квадратных сантиметров. Средняя линия фигуры равна 5 см. Нужно найти высоту по формуле. h = (2S) / m, h = (2 х 30) / 5, h = 60 / 5, h = 12 см. 12 см – высота трапеции.
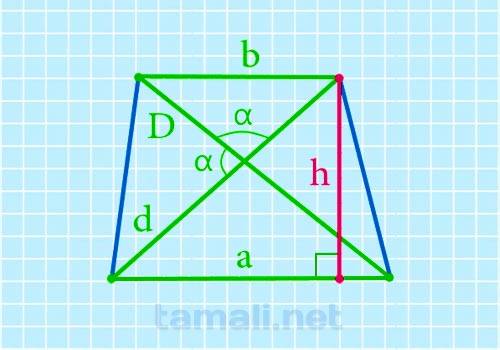
Для нахождения высоты трапеции при помощи известного основания, диагонали и углу между диагоналями используют нижеприведенную формулу:
где h — это искомая высота трапеции, D и d — известные диагонали, a и b — длины обеих оснований, sin(α) — угол между диагоналями.
Пример. Закрепим на примере: В трапеции ABCD диагонали равны 10 см каждая. Известно, что сумма основ фигура равна 20 см. Угол, созданный между диагоналями – 30 градусов. Нужно найти высоту. Для этого нужно воспользоваться выше предоставленной формулой. h = ((Dd) / (a+b)) x sin (α), h = ((10 х 10) / (20)) x sin (30), h = 5 x sin (30), h = 2.5 см. Высота трапеции равна 2.5 см
Можно выделить 2 разновидности трапеции:
Высотой трапеции принято называть отрезок, которой показывает самое короткое расстояние между верхним и нижним основанием фигуры. Существует большое количество математических задач разного уровня сложности, для решения которых активно применяют высоту. Стоит разобраться со всеми возможными формулами, которые используются для нахождения высоты трапеции.