Вычислить среднюю линию трапеции онлайн

Термин «трапеция» произошёл от греческого слова «столик». В русском языке от того же слова произошло понятие «трапеза» — еда.

Средняя линия — отрезок, который прокладывается через противолежащие стороны, и который дробит их точно на половинки.

Средняя линия трапеции имеет три отличительных черты:

• Она параллельна базовым сторонам четырёхугольника;
• Эквивалентна половинке суммирования оснований;
• Разбивает первоначальный четырёхугольник на две поменьше. Вместе с тем их площади имеют конкретное соотношение друг к другу.

Через длины оснований

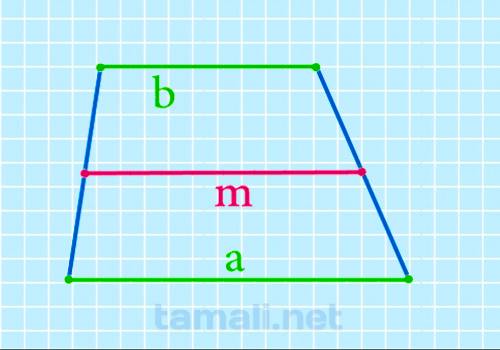
Имеется одно основная формулировка, которая позволяет рассчитывать величину средней линии. Величина средней линии будет равна сумме базовых сторон фигуры, поделённой напополам. Формула следующая:

где a и b — наибольшая и наименьшая стороны.

Пример. Если наибольшая базовая сторона равна 8, а наименьшая — 10, то (8 + 10) / 2 = 9. Или, если наибольшая базовая сторона равна 15, а наименьшая — 3. Тогда:
(3 + 15) / 2 = 9.

Через площадь и высоту

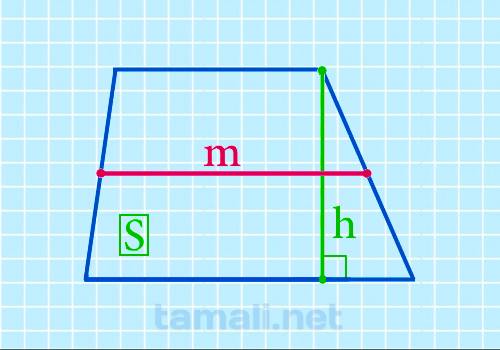
Формулировка поиска величины срединного отрезка через площадь и перпендикуляр:

где S — площадь, h — перпендикуляр.

Пример. Если площадь равняется 20, а высота — 5, тогда: M = 20 / 5 = 4. Если площадь равна 50, а высота равна 5, тогда срединный отрезок:
M = 50 / 5 = 10.

Через верхнее основание, высоту и углы при нижнем основании

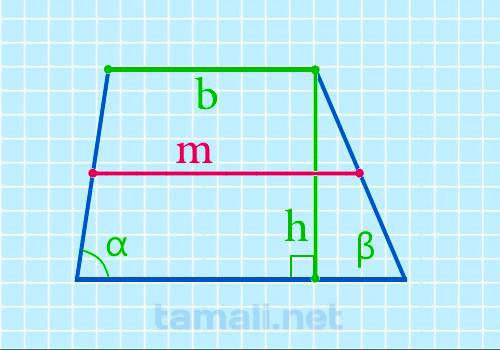
Равенство расчёта величины срединного отрезка через наибольшую базовую сторону, высоту и углы при наименьшей базовой стороне выглядит:

где b — наибольшая базовая сторона, α и β — углы при наименьшей базовой стороне, h — высота.

Пример. Наибольшая сторона равняется 15, высота — 6, а углы — 45 и 30. В таком случае:
m = 15 + 6 · (ctg 45 + ctg 30)/2 = 15 + 6 · (1 + √3)/2 ≈ 23,196.

Через диагонали, высоту и угол между диагоналями

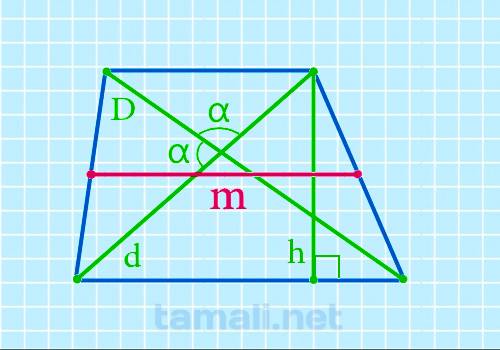
Формулировка исчисления величины срединного отрезка через диагонали, высоту и уголок между диагоналями описывается:

где d1, d2 — диагонали, α — уголок между диагоналями, h — высота.

Пример. Пусть диагонали четырёхугольника равняются 15 и 4, высота — 5, а уголок между диагоналями фигуры — 30 градусов. Значит:
m = (15 * 4)/(2 * 5) * sin 30 = 6 * 1/2 = 3.

Если в качестве диагоналей взять 20 и 5, высоты — 6, а угла — 30, тогда: m = (20 * 5)/(2 * 6) * sin 30 ≈ 8,33 * 1/2 ≈ 4,167.

Через нижнее основание, высоту и углы при нижнем основании

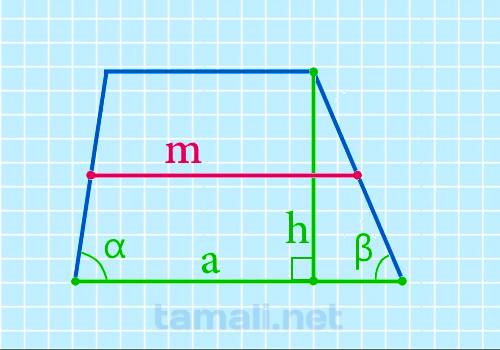
Формулировка нахождения величины срединного отрезка через наименьшую базовую сторону, высоту и углы при наименьшей базовой стороне приведена далее:

где a — наименьшая базовая сторона, α и β — углы при наименьшей базовой стороне, h — высота четырёхугольника.

Пример. Если наименьшая базовая сторона четырёхугольника равносильна 5, углы — 45 и 45, а высота — 2, тогда: 5 – 2 · (ctg 45 + ctg 45)/ 2 = 3.

Через боковые стороны, верхнее основание и углы при нижнем основании

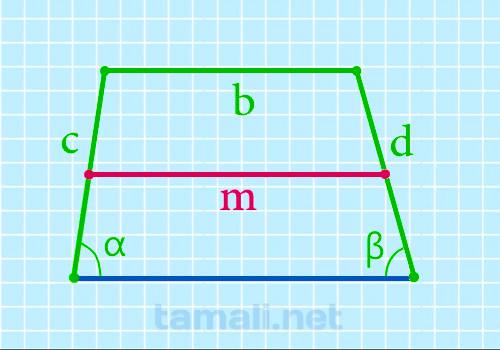
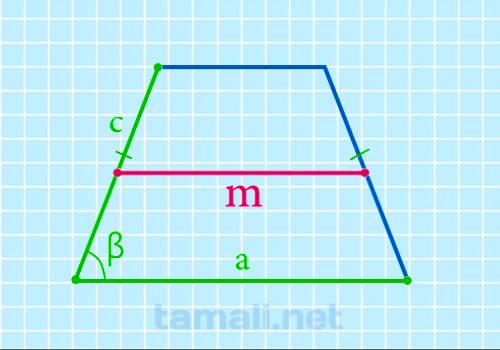
Тождество поиска величины срединного отрезка через вспомогательные стороны, наибольшую сторону и углы при наименьшей стороне:

где b — наибольшая сторона, c и d — вспомогательные стороны, α и β — углы при наименьшей стороне.

Пример. Если в качестве наибольшей стороны взять 15, наклонных сторон — 7 и 9, а углов при наименьшей стороне — 60 и 60 градусов. Следовательно: m = (2 * 15 + 7 * cos 60 + 9 * cos 60) / 2 = (30 + 3,5 + 4,5) / 2 = 19.

Через боковые стороны, нижнее основание и углы при нижнем основании

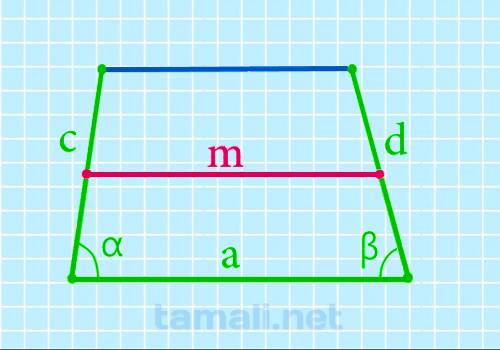
Выражение исчисления величины срединного отрезка через вспомогательные стороны, меньшую сторону и углы при меньшей стороне:

где a — меньшая сторона, c и d — наклонные стороны, α и β — углы.

К примеру, если нижняя сторона равна 8, боковая сторона 5, а угол при нижней стороне фигуры — 60, тогда:
m = (2 · 8 – 2 · 5 · cos 60) / 2 = 3.

Если же нижняя сторона равняется 12, боковая сторона 6, а угол при нижней стороне — 60, в таком случае:
m = (2 · 12 – 2 · 6 · cos 60) / 2 = 9.

Средняя линия равнобедренной трапеции через боковую сторону, верхнее основание и угол при нижнем основании

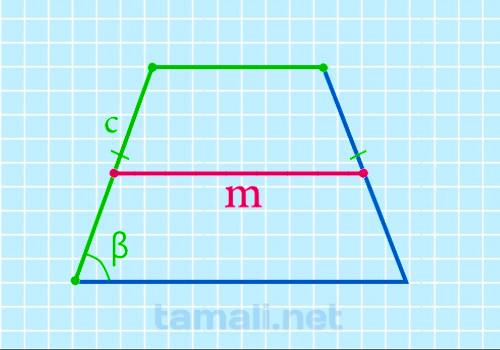
Формула расчёта длины срединного отрезка через боковые стороны, верхнюю сторону и углы при нижней стороне:

где b — верхняя сторона, c — боковая сторона четырёхугольника, β — угол.

Например, если верхняя сторона четырёхугольника равняется 5, боковая сторона 8, а угол при нижней стороне фигуры — 60, тогда срединный отрезок рассчитывается следующим образом: m = (2 · 5 – 2 · 8 · cos 60) / 2 = 1.

Если представить верхнюю сторону длиной 6, боковую сторону длиной 5, а угол при нижней стороне четырёхугольника — 60, в таком случае: m = (2 · 6 – 2 · 5 · cos 60) / 2 = 3,5.

Через боковые стороны, нижнее основание и углы при нижнем основании

Выражение исчисления величины срединного отрезка через вспомогательные стороны, меньшую сторону и углы при меньшей стороне:

где a — меньшая сторона, c и d — наклонные стороны, α и β — углы.

К примеру, если нижняя сторона равна 8, боковая сторона 5, а угол при нижней стороне фигуры — 60, тогда: m = (2 · 8 – 2 · 5 · cos 60) / 2 = 3.

Если же нижняя сторона равняется 12, боковая сторона 6, а угол при нижней стороне — 60, в таком случае: m = (2 · 12 – 2 · 6 · cos 60) / 2 = 9.

Средняя линия прямоугольной трапеции через нижнее основание, высоту и острый угол при нижнем основании

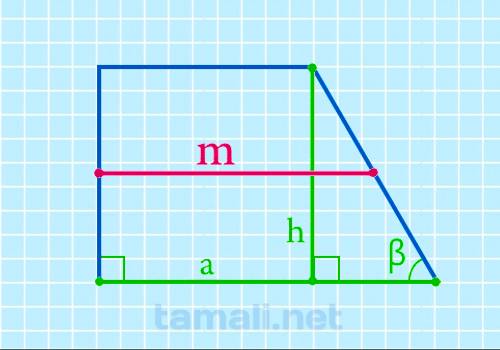
Формула определения длины срединного отрезка через боковые стороны, верхнюю сторону и углы при нижней стороне:

где a — нижняя сторона, h — высота, β — острый уголок при нижней стороне.

Пример. Пусть нижняя сторона четырёхугольника равняется 8, высота — 3, а острый уголок — 45, в таком случае: m = 8 – 3 · ctg 45 / 2 = 6,5.

Средняя линия прямоугольной трапеции через верхнее основание, высоту и острый угол при нижнем основании

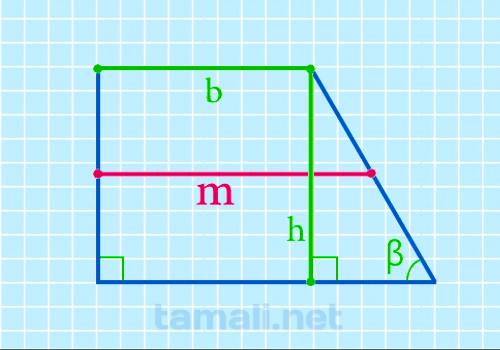
Формула определения длины срединного отрезка через боковые стороны, верхнюю сторону и углы при нижней стороне:

где b — верхняя сторона, h — высота, β — острый угол при нижней стороне.

Пример. В качестве верхнего возьмём 4, высоты — 2, острого угла — 45. В таком случае формула такая: m = 4 + 2 · ctg 45 / 2 = 5.

Общее понятие трапеции

Трапеция — геометрическая фигура, четырёхугольник, две противолежащие стороны которого размещены на параллельных прямых. В свою очередь, две иные стороны должны быть не параллельными. Нередко в описании четырёхугольника не обращают внимания на завершающее требование.

Впервые эту фигуру описал математик Древней Греции Евклид в своих работах. В своей книге «Начала» он таким образом характеризует всякий четырёхугольник, не являющийся параллелограммом.

Описывая трапецию, необходимо выделить следующие элементы:

• Параллельные противолежащие стороны именуются основаниями фигуры;
• Две иные стороны именуют боковыми или наклонными сторонами;
• Отрезок, который объединяет средины вспомогательных сторон, прозвали средней линией четырёхугольника;
• Углом при основании трапеции прозвали её внутренний уголок, который образовало основание с наклонной стороной.

Выделяют такие характеристики трапеции:

1. Срединный отрезок трапеции пролегает параллельно основаниям и равняется половине их суммирования;
2. Отрезок, который объединяет средины диагоналей трапеции, равняется половинке разности оснований и пролегает по средней линии;
3. Отрезок, который параллелен основаниям и пролегает через точку скрещивания диагоналей, разделяется последней напополам и равняется 2xy / (x + y) среднему гармоническому (один из методов, которым можно характеризовать «среднюю» величину определённой совокупности чисел) величин оснований трапеции;
4. В трапецию можно вписать окружность, если суммирование величин оснований четырёхугольника равняется суммированию величин её вспомогательных сторон;
5. Точка скрещивания диагоналей трапеции, точка скрещивания последующих продлений её вспомогательных сторон и средины оснований располагаются на единой прямой;
6. Если суммирование углов при одном из оснований трапеции равняется 90°, в таком случае продолжения наклонных сторон перекрещиваются под прямым углом, а отрезок, объединяющий средины оснований, равняется половинке их разности;
7. Диагонали четырёхугольника разделяют его на четыре треугольника. Два из них, которые прилегают к основаниям, подобны. Два иных, которые прилегают к вспомогательным сторонам, имеют равную площадь;
8. Если отношение оснований равно K, тогда отношение площадей треугольников, которые прилегают к ним, равняется K²;
9. Прямая Ньютона (прямая, которая объединяет серединки диагоналей четырёхугольника) для четырёхугольника сходится с её срединным отрезком.

Рассмотренная версия трапеции — это наиболее популярная разновидность геометрической фигуры. Однако, выделяют и дополнительные ситуации.

Равнобедренная или равнобокая или равнобочная трапеция — та, у которой наклонные, иными словами, непараллельные, стороны равняются друг другу. В евклидовой геометрии равнобедренной трапецией именуется выпуклый четырёхугольник с осью симметрии, которая пролегает через средины двух противолежащих сторон. Во всякой равнобедренной трапеции два противолежащих основания параллельны, две наклонные стороны имеют одинаковые величины (характеристика, которой параллелограмм также соответствует). Диагонали также имеют равносильные величины. Углы при всяком основании равняются друг другу и углы при разнообразных основаниях считаются смежными, иначе говоря, в сумме составляющие 180 градусов.

Трапеция является равнобедренной лишь в том случае, когда выполняется одно из таких эквивалентных условий:

• Прямая, пролегающая через средины оснований, ортогональна ним;
• Перпендикуляр, который проложен из вершины на наиболее протяжённое основание, разделяет его на две части, одна из которых равняется половине суммирования оснований, а другая — половинке разности;
• Углы при всяком основании равносильны;
• Суммирование противолежащих углов равняется 180 градусам;
• Величины диагоналей равносильны;
• Вокруг следующего четырёхугольника можно описать окружность;
• Вершинами подобного четырёхугольника ещё считаются вершины какого-либо антипараллелограмма или контрпараллелограмма (плоского четырёхугольника, где всякие две противолежащие стороны равняются друг другу, но не параллельны, в сравнении с параллелограммом);
• Если в равнобедренной трапеции диагонали ортогональны, тогда перпендикуляр равняется половине суммирования базовых сторон.

Диагонали равнобедренной трапеции равносильны. Иными словами, всякая равнобедренная трапеция считается равнодиагональным четырёхугольником. Тем не менее диагонали равнобедренной трапеции разделяются в одинаковой пропорции.

Прямоугольная трапеция — та, где одна из наклонных сторон и основание формируют прямой угол (в 90 градусов).

Иным особенным случаем считается трапеция с тремя равносильными сторонами. В иностранной литературе её именуют трёхсторонней трапецией или триравнобедренной трапецией. Подобный четырёхугольник анализируется как отсечение четырёх последовательных вершин от правильного многоугольника, который имеет пять или больше сторон.

По заданному описанию параллелограмм и прямоугольник — особые случаи трапеции. Тем не менее при применении подобного термина основная доля характеристик равнобедренной трапеции становится недействительна, так как параллелограмм становится её особым случаем.

Анализирование трапеции неразрывно связано с окружностью:

1. Если суммирование базовых сторон трапеции равносильно суммированию вспомогательных сторон, то в неё можно вписать окружность. Средняя линия в такой ситуации равносильна суммированию наклонных сторон, разделённой на два, ведь средняя линия трапеции равносильна половинке суммирования оснований;
2. В четырёхугольнике его вспомогательная сторона различима из центра вписанной окружности ортогонально;
3. Если четырёхугольник можно вписать в окружность, в такой ситуации она равнобедренная.