
Треугольник – это фигура, имеющая три стороны и три угла. Если один из углов треугольника равен 90°, то он называется «прямоугольным». При этом две стороны, образующие прямой угол – это катеты. Гипотенуза – это третья сторона, которая находится напротив прямого угла и соединяет катеты между собой, образуя замкнутую геометрическую фигуру.
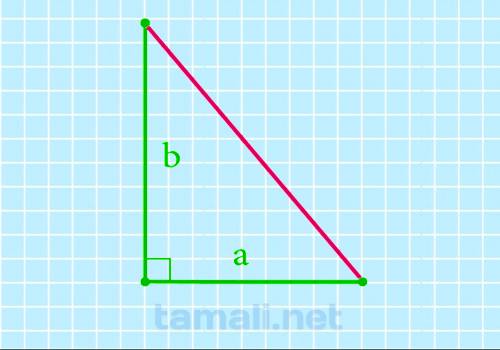
Если в геометрической фигуре известна длина катетов, то можно вычислить площадь фигуры через них. В некоторых учебниках вертикальный катет называется высотой и обозначается буквой h, но это не обязательно. При написании формулы можно использовать буквенные обозначения a и b.
Один из самых простых линейных вариантов вычисления — через две стороны, то есть через два катета, прилегающих к прямому углу. В этом случае площадь равна половине произведения катетов.
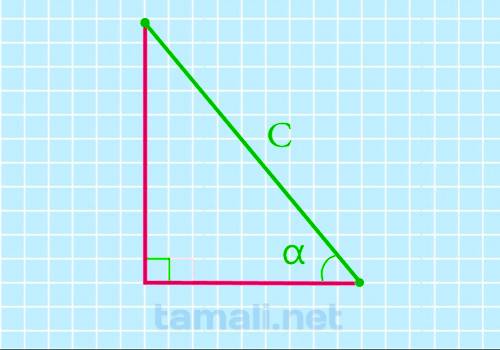
Так как один угол, от которого отходят два катета «а» и «b» равен 90°, два остальных будут острыми. Эти углы образуются в местах соединения катетов с гипотенузой. Для того, чтобы рассчитать итоговую S по гипотенузе и острому углу, нужно сначала через длину сторон вычислить sin (синус) и cos (косинус). Углы в прямоугольном треугольнике обозначаются греческими буквами α (альфа) – угол 90° и β (бетта) – один из острых углов. Если удается вычислить sin и cos, то через них можно вычислить площадь по следующей формуле:
Чтобы вычислить sin α, нужно сторону фигуры «a» (то есть высоту) разделить на гипотенузу: sin α= a / c.
Чтобы вычислить cos α, нужно сторону «b» разделить на гипотенузу: cos α= b / c.
В данных формулах гипотенуза обозначается буквой «с». Таким образом выглядят формулы sin и cos для угла α. Точно таким же образом можно сделать расчеты и для угла β, но даже это не обязательно, потому что в прямоугольном треугольнике cos α = sin β, а sin α = cos β.
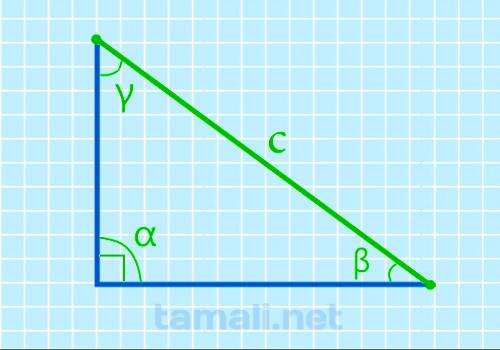
Для данного расчета также понадобятся синусы всех углов треугольника. Нужно вычислить по уже знакомым
формулам sin α= a / c и sin β= b / c. Также понадобится синус третьего угла, который обозначается
греческой буквой γ (гамма). Синус угла γ рассчитывается из разницы между суммой всех углов (180°)
треугольника и суммы двух других углов, а именно: sin (γ) = 180 – (α + β). Также понадобится длина
гипотенузы, которая будет обозначена буквой «C».
Исходя из всех известных величин, формула
площади треугольника через гипотенузу и острый угол следующая:
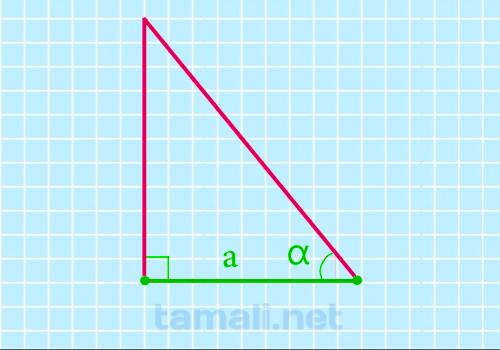
Зная длину катетов, также можно легко вычислить площадь, но в два этапа. Для этого понадобится предварительно найти tg (тангенс) одного из углов. Например, tg α можно рассчитать по формуле tg α = a/b, где «a» – это высота (вертикальный катет), а «b» – второй (горизонтальный) катет. Для того, чтобы вычислить tg угла β, в формуле нужно поменять местами стороны: tgβ = b/a.
Так, формула вычисления площади прямоугольника через катет и острый угол выглядит следующим образом: если известна сторона «а» —
Если известна сторона «b», то вместо a подставить b.
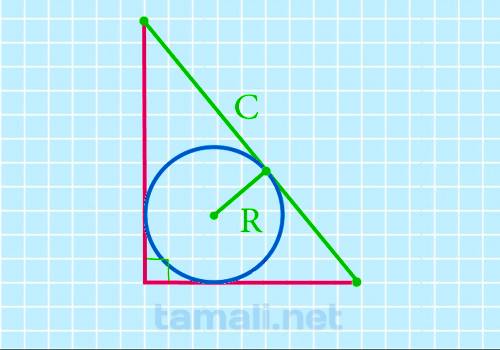
Внутри вписанного круга есть точка (центр круга), которая равноудалена от обоих катетов и гипотенузы. Прямая от этой точки и до катета, проведенная под прямым углом, — это r (радиус) окружности. Математически его можно рассчитать по формуле r = (a + b – c) / 2. После того, как радиус стал известен, площадь можно вычислить через него:
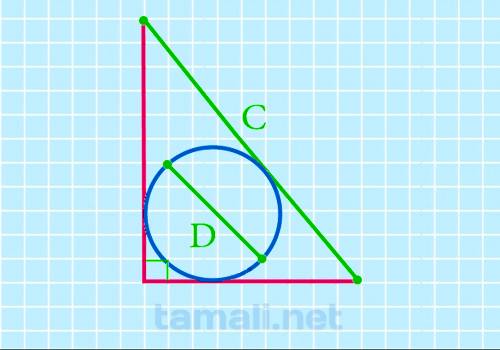
Если d (диаметр) вписанного круга неизвестен, его можно рассчитать следующим образом: d = a + b – c. Если в условии задачи известен радиус r вписанной окружности, то для вычисления диаметра его можно умножить на 2, так как d = 2r. Формула площади при известном размере диаметра будет следующая:
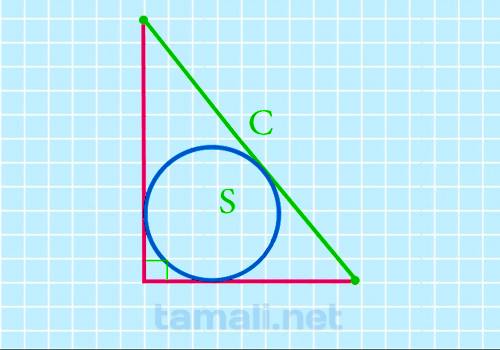
Для этой формулы понадобится знать площадь вписанного круга. Если в условиях задачи она неизвестна, но вычисляется она по следующей формуле: S = π · r², где π – это математическая константа, равная в сокращении 3,14, а r – радиус круга. Таким образом, зная площадь круга, можно рассчитывается площадь треугольника:
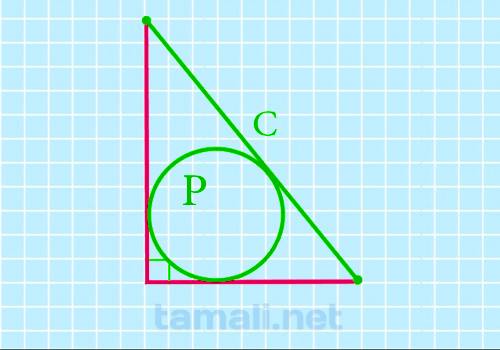
Чтобы найти периметр окружности для главной формулы площади треугольника, нужно знать либо диаметр
окружности, либо радиус. Периметр в данном случае обозначается латинской буквой P. Формулы буду
следующие: если известен диаметр окружности P = d · π, если известен радиус окружности P = 2 · r ·
π.
Зная периметр вписанной окружности, можно рассчитать площадь прямоугольного треугольника по
следующей формуле:
где C – это гипотенуза треугольника, π – это математическая константа, равная в сокращении 3,14, и периметр окружности P.
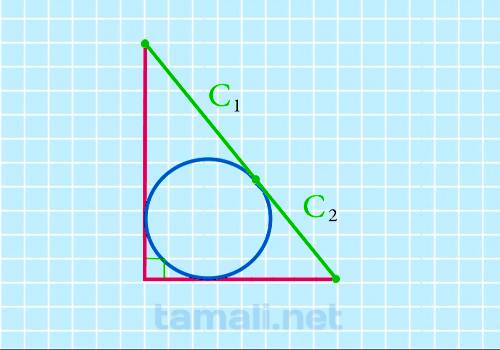
Если внутри прямоугольного треугольника нарисовать окружность, центр которой будет равноудален от катетов и гипотенузы, она разделит гипотенузу на два отрезка, которые условно обозначаются С1 и С2. С их помощью, не зная других величин, можно вычислить площадь треугольника:
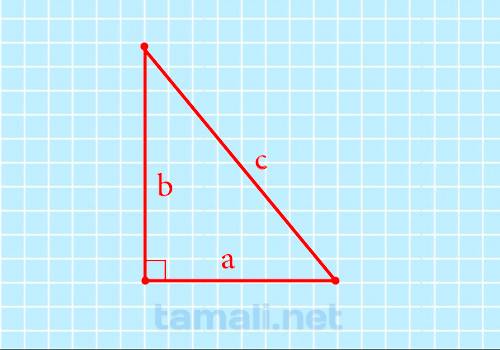
Для вычисления площади по методу Герона понадобится значение полупериметра, который обозначается маленькой латинской буквой «p» (полный периметр обозначается заглавной Р). Полупериметр – это половина суммы всех сторон, а именно: p = (a + b + c)/2, где a и b – это катеты, а С – гипотенуза.
После того, как полупериметр вычислен, можно переходить к основной формуле площади прямоугольного треугольника. Для того, чтобы ее найти, нужно рассчитать корень квадратный из следующих величин:
Герон Александрийский был математиком во времена Римской империи. Одним из направлений его деятельности была так называемая «Метрика» и ее подраздел «Геометрика», по которым ученый написал большую энциклопедию. В содержании этой книги, в том числе, была также формула вычисления площади прямоугольного треугольника по длинам его сторон. Впервые этот метод определения площади был установлен еще Архимедом, но конкретную формулу вывел именно Герон, предположительно в I веке до н.э.
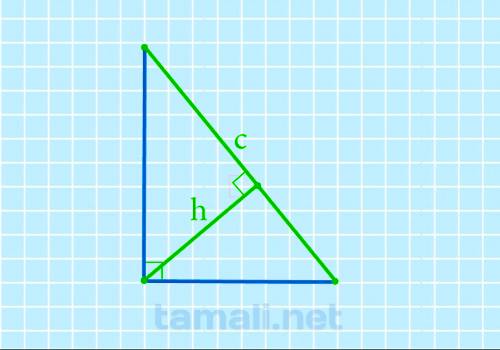
Высота – это прямая, соединяющая точку пересечения катетов с гипотенузой под углом 90°. При этом высота разделяет прямоугольный угол треугольника на два равных по 45° каждый. Обозначается данная величина латинской буквой h. Формула площадки треугольника через гипотенузу и высоту простая и линейная:
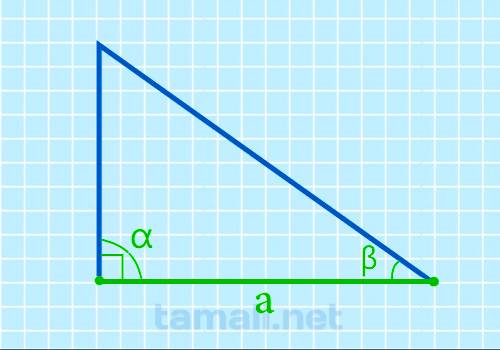
Для составления данной формулы нужно определиться с наименованием сторон и углов. Например, нижний катет треугольника (горизонтально расположенный), будет называться стороной «a». Слева от него находится прямой угол в 90°, под условным обозначением α, а справа от катета «a» находится прилегающий острый угол β.
Для итоговой формулы также понадобятся синусы углов. Таким образом, sin α= a / c и соответственно sin β= b / c. После того, как эти величины будут найдены, можно переходить к основной формуле:
где 180° — это сумма всех углов треугольника.
Площадь прямоугольных треугольников напрямую связана с вычислением площади прямоугольников, так как в них обоих присутствуют углы в 90°. При этом для вычисления нужной величины, можно использовать любой из вышеперечисленных способов. Выбор зависит только от наличия известных параметров геометрической фигуры или от выбора самого простого решения. Для того, чтобы уметь пользоваться формулой, нужно понять логическую цепочку ее вывода и, если не все составляющие уравнения известны, найти способ их узнать через дополнительные формулы. Зная определенные параметры треугольника, путем различных вычислений можно рассчитать его площадь.