Здесь рассмотрены все возможные способы нахождения высоты треугольников разных типов. Высота треугольника – отрезок, проведенный из вершины треугольника перпендикулярно к противоположной стороне. В задачах нахождение высоты часто является промежуточным звеном для поиска других значений. Она и является катетом в треугольнике, который сама же образует, и участвует во многих формулах, например, для нахождения площади.
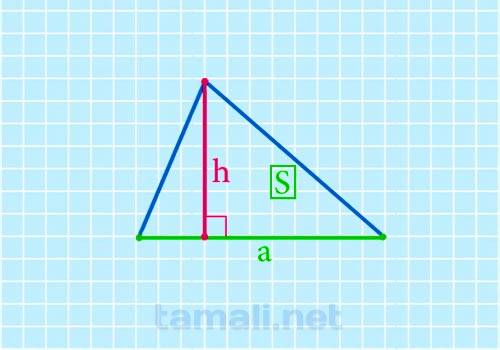
Через площадь и длину высота находится по формуле:
где S – площадь треугольника, а – сторона треугольника.
Согласно этой формуле высота равна удвоенной площади, деленной на длину стороны, к которой она проведена.
Пример. Найдите высоту разностороннего треугольника, проведенную к стороне а, площадь которого равна 27 см, а длина стороны а составляет одну треть от площади. Решение: Найдем сторону а. Так как известно, что она составляет треть от площади, а = 27 / 3 = 9 см. Теперь воспользуемся формулой для нахождения высоты: h = 2S / a. Подставим известные значения. h = 2 * 27 / 9 = 6 см. Ответ: 6 см
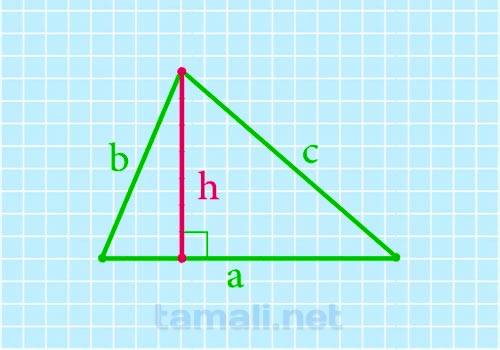
Через длины всех сторон высота разностороннего треугольника ищется по формуле:
где h – высота, а, b, c – стороны треугольника, p – полупериметр треугольника.
Полупериметр треугольника можно найти либо в два этапа через периметр, либо сразу по формуле. Этим способом удобно пользоваться, когда треугольник разносторонний.
Пример. Периметр разностороннего треугольника равен 18 см. Длины сторон 6 см и 8 см. Найдите высоту, проведенную к стороне а. Решение: P = a + b + c, значит с = P – a – b , то есть c = 18 – 8 – 6 = 4 см. Для нахождения h будем использовать формулу h = (2 √(p (p-a)(p-b)(p-c))) / 2. Сначала найдем полупериметр (p): p = p / 2 = 18 / 2 = 9 см. Подставим, найденные значения в формулу высоты: h = (2 √(9 (9 — 6)(9 — 8)(9 — 4))) / 2 = √135 / 3 = 2,12 см
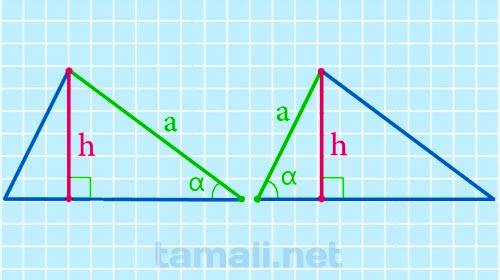
Через длину прилежащей стороны и синус угла высота ищется по следующей формуле:
где а – длина стороны, sin α – синус прилежащей стороны.
Пример. В разностороннем треугольнике высота проведена к стороне AB. Угол ACH равен 30˚, а длина стороны AB 12 см. Найдите длину высоты CH в треугольнике ABC. По теореме о сумме углов в треугольнике найдем угол САН. ∠САН = 180 – (∠АСН + ∠АНС). ∠САН = 180 – 90 – 30 = 60˚ sin 60º = 1/2. СН = AB * sin ∠САН, СН = 12 * 1/2 = 6 см. Ответ: 6 см
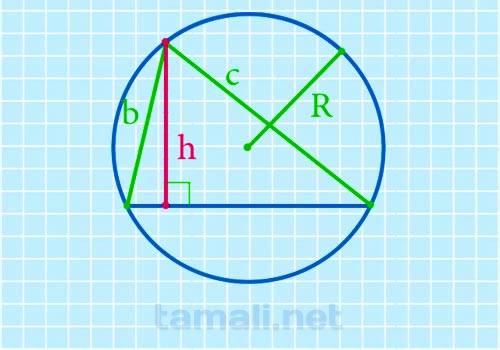
Через стороны и радиус описанной окружности высоту можно найти по следующей формуле:
где r – радиус описанной около треугольника окружности, b,c – стороны треугольника
Пример. Вокруг разностороннего треугольника описана окружность с радиусом 3 см. Из вершины между сторонами b и с проведена высота. Стороны b и с соответственно равны 5 см и 6 см. Найдите высоту. Решение: Найдем высоту, используя формулу h = 5 * 6 / 2 * 3 = 30 / 6 = 5 см. Ответ: 5 см.
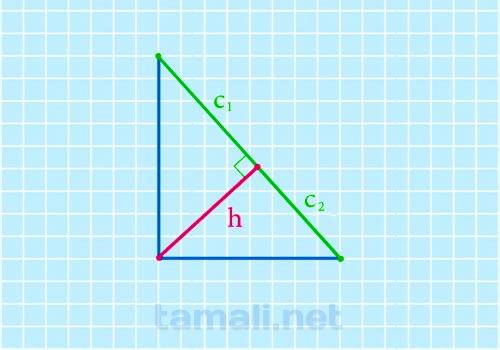
Через длины отрезков образованных на гипотенузе высоту можно найти по следующей формуле:
где: C1, C2 — отрезки, образованные проведением высоты к гипотенузе.
Пример. В прямоугольном треугольнике катеты равны 4 см и 3 см. Угол BAH равен 30˚. Найдите высоту. По теореме Пифагора найдём сторону BC, которая является гипотенузой в треугольнике ABC. BC² = AB² = AC², BC² = 4² + 3² = 16+9 = 25 см², BC = √25 = 5 см. Угол АНВ равен 90˚, так как АН является высотой, то есть, проведена перпендикулярно к стороне ВС. Следовательно, треугольник АНВ – прямоугольный. Сторона ВН лежит напротив угла 30˚ в прямоугольном треугольнике, значит, ее длина равна половине длины гипотенузы. Найдем ВН. BH = 1/2 AB. BH = 1/2 × 4 = 2 см. BC = BH + HC, значит, HC = BC – BH, HC = 5 – 2 = 3 см. По формуле найдем высоту (АН). АН = √(2 * 3) = √6 = 2,4 см. Ответ: 2,4 см.
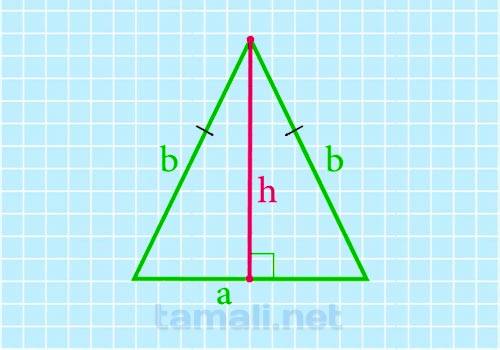
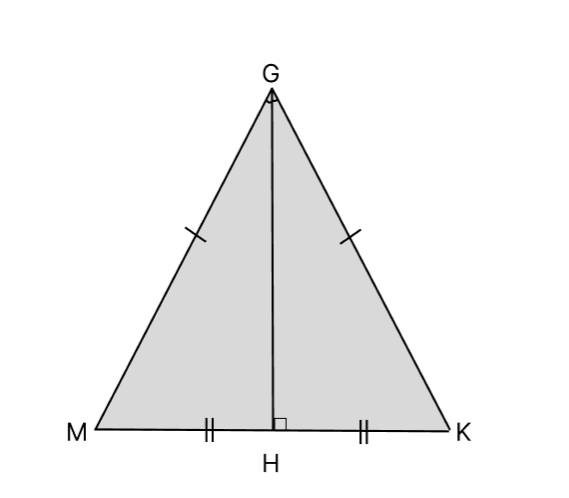
Через основание и боковые стороны высота равнобедренного треугольника находится по формуле:
где а – основание треугольника, b – боковая сторона. Для равнобедренного треугольника.
Пример. В равнобедренном треугольнике АВС боковая сторона равна 8 см. Из вершины В к основанию АС проведена высота ВН. Отрезок АН равен 5 см. Найдите высоту. Решение: Так как по условию треугольник АВС равнобедренный по условию, то АВ = ВС = 8 см высота ВН, является и медианой, и биссектрисой. Значит, АН = НС, а АС = НС + АН, АС = 5 + 5 = 10 см. По формуле найдем высоту ВН = √(АВ² — АС² / 4). ВН = √(8² — 10² / 4) = √(64 — 100 / 4) = √39 = 6 см. Ответ: 6 см.
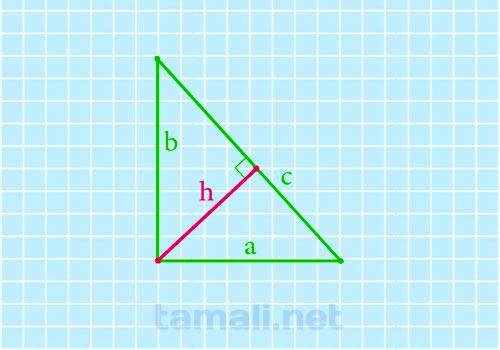
Если известны все стороны прямоугольного треугольника, то можно найти его высоту по следующей формуле:
где a,b,c – стороны треугольника.
Пример. В прямоугольном треугольнике угол между катетом и гипотенузой равен 45˚. Длина стороны АС равна 6 см. Найти высоту АН. Решение: По теореме о сумме углов в треугольнике найдем угол АСВ. ∠АСВ = 180˚ – (45˚ + 90˚) = 45˚. Так как АСВ = АСВ, то треугольник АВС равнобедренный с основанием ВС. Таким образом, АС = АВ = 6 см. По теореме Пифагора найдем гипотенузу ВС. BC² = AB² + AC². BC² = 6² + 6² = 36 +36 = 72 см². ВС = √72 = 6√2 см. Найдем высоту по формуле AH = AB * AC / BC. АН = 6 * 6 / 6√2= см. Домножим полученное значение на √2: (6 * √2) / √2 * √2 = 6√2 / 2 = 3√2 см. Ответ: 3√2 см
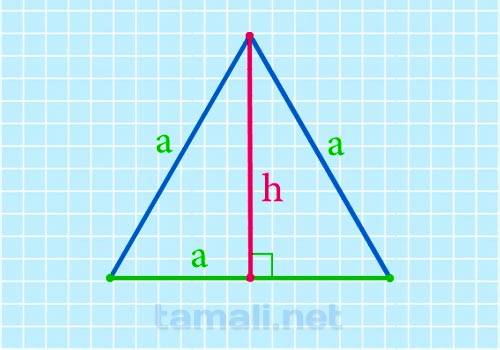
Высота равностороннего треугольника через сторону треугольника ищется по следующей формуле:
где a – сторона треугольника.
Пример: Найдите высоту в равностороннем треугольнике, если известно, что его сторона равна 4√3 см. Решение: Для нахождения высоты воспользуемся формулой h = a√3 / 2 = √3 * 4 √3 / 2 = 4 * 3 / 2 = 6 см. Ответ: 6 см
В зависимости от типа треугольника высота может располагаться по-разному: