
Треугольник — геометрическая фигура, составленная из трёх отрезков. Они объединены тремя точками, не лежащие в единственной прямой. Такие отрезки обычно именуют сторонами, а заданные точки — вершинами. Средняя линия такого многоугольника — отрезок, объединяющий средины двух сторон.
Во всяком треугольнике можно проложить три средних линии. В прямоугольном многоугольнике такой отрезок равняется половине основания. Средняя линия прямоугольного треугольника разделяет его на четыре прямоугольных треугольника. Существует и признак срединного отрезка треугольника: если отрезок в многоугольнике пролегает через средину одной из его сторон, пересекает вторую и параллелен ей, тогда такой отрезок называется средней линией.
Выделяют свойства срединного отрезка:
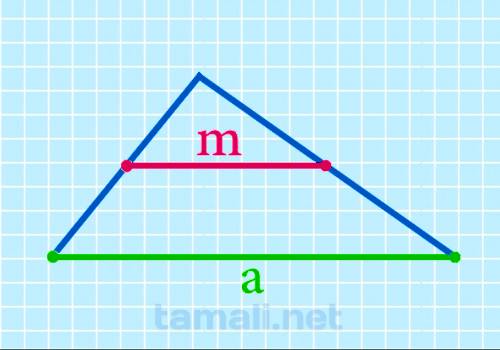
Срединный отрезок равняется половине противолежащей стороны. Следовательно, формула выглядит так:
где a — противолежащая сторона.
Следовательно, если такая сторона будет равна 50, то срединный отрезок будет равен m = 50/2 = 25. Если же сторона будет равна 20, тогда срединный отрезок будет рассчитываться так: m = 20/2 = 10.
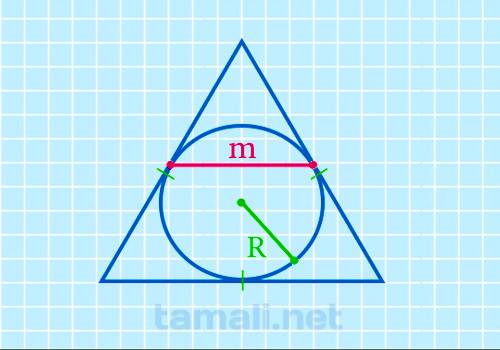
Срединный отрезок равностороннего многоугольника через радиус вписанной окружности высчитывается так:
где r — радиус вписанной окружности.
Таким образом, если радиус такой окружности равняется 5, тогда m= 5√3 ≈ 8,66. Если же радиус будет равен, допустим, 9, в таком случае m = 9√3 ≈ 15,59.
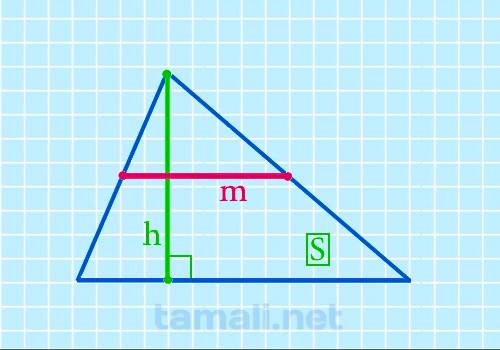
Срединный отрезок многоугольника равен частному площади и высоты, перпендикулярной этой средней линии. Таким образом, тождество имеет такой вид:
где S — это площадь, а h — перпендикуляр, ортогональный срединному отрезку.
Если площадь некоторого многоугольника будет равна 25, а перпендикуляр — 5, тогда m = 25/5 = 5. Если же в качестве площади взять число 60, а в качестве перпендикуляра — 3, получится следующий срединный отрезок: m = 60/3 = 20.
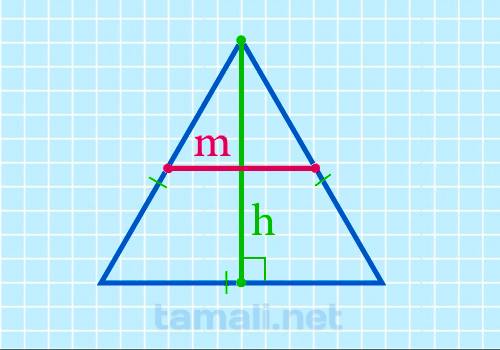
Срединный отрезок равностороннего многоугольника через перпендикуляр высчитывается следующим образом:
где h — перпендикуляр равностороннего многоугольника.
К примеру, если перпендикуляр равностороннего многоугольника равен 5, тогда срединный отрезок будет
такой: m = 5/√3 ≈ 2,89.
Если же перпендикуляр будет равен 10, тогда
срединный отрезок будет около m = 10/√3 ≈ 5,77.
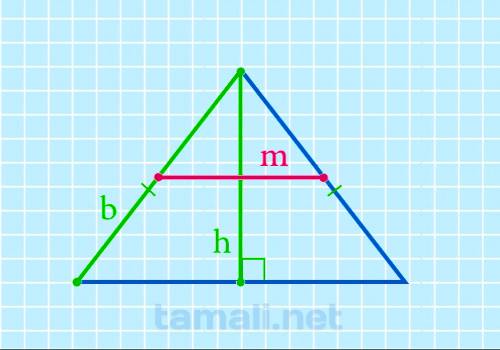
Срединный отрезок равнобедренного многоугольника через боковую сторону и высоту вычисляется следующим образом:
где a — боковая сторона, а h — перпендикуляр.
Допустим, если боковая сторона многоугольника равна 5, а перпендикуляр — 3, тогда m = 25 – 9 = 16.
Если же в качестве боковой стороны взять число 8, а в качестве перпендикуляра равнобедренного
многоугольника — 2, в таком случае m = 64 – 4 = 60.
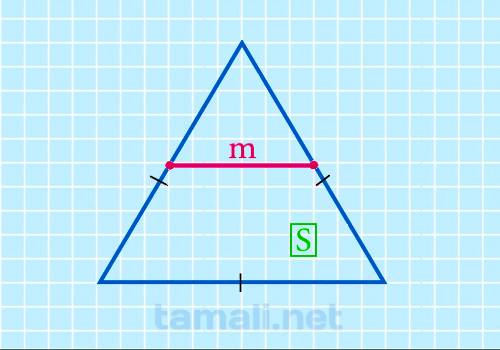
Срединный отрезок равнобедренного многоугольника через площадь находится по следующей формуле:
где S — это площадь равностороннего многоугольника.
Допустим, если площадь равностороннего многоугольника будет равна 5, тогда m = 1/4 √(√3/5) ≈ 0,15.
Если выбрать равносторонний многоугольник побольше, к примеру, с площадью 25, в таком случае m = 1/4 √(√3/25) ≈ 0,065.
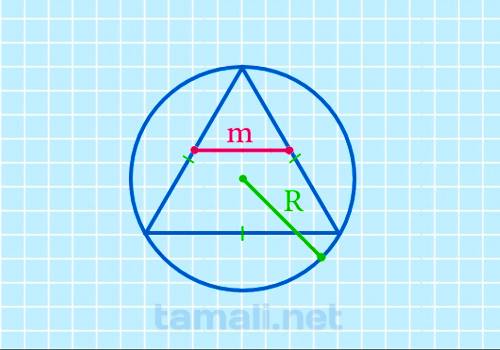
Срединный отрезок равностороннего многоугольника через радиус описанной окружности высчитывается так:
где R — радиус описанной окружности.
Следовательно, если радиус такой окружности будет равен 15, тогда m = 15√3/2 =12,99. Если в качестве радиуса взять число 24, в таком случае m = 24√3/2 = 20,78.
Средняя линия фигур в планиметрии — отрезок, который объединяет средины двух сторон представленной фигуры. Такой термин используется при описании треугольников, четырёхугольников и трапеций. В некоторых случаях рассматривается вырожденный треугольник, три вершины которого пролегают на единственной прямой. Треугольник считается одной из основных геометрических фигур, повсюду применяемых в науке и технике, потому изучение его качеств велось с давних времён.