
Шаровой сектор – это часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью, основанием которой служит основание сегмента, а вершиной центр шара. Другое определение исходит из того, что шаровой сектор – тело вращения, т.е. образовано вращением какой-либо плоской и ограниченной кривой геометрической фигуры вокруг лежащей в той же плоскости оси. Объем шарового сегмента определяется рядом его размеров, ниже 2 формулы для вычисления объема.
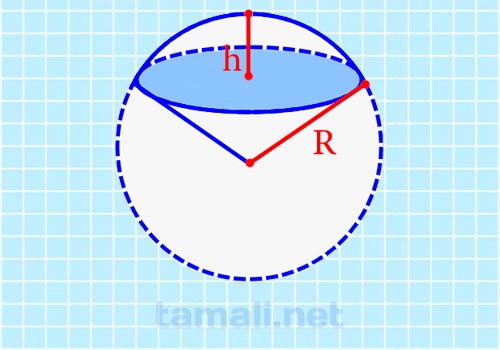
Зная радиус и высоту шарового сектора, можно найти его объем по следующей формуле:
где R – радиус шара, h – высота шарового сегмента (или проекция хорды, стягивающей дугу сектора, на ось вращения).
Значение π примерно равно 3,14 – это числовая постоянная «число пи», одна из самых известных и чаще всего использующихся, равная отношению длины окружности к ее диаметру; для всех окружностей это отношение постоянно. «Пи» число иррациональное и трансцендентное, т.е. не может быть выражено никакой рациональной дробью и не может быть корнем какого-либо многочлена с целыми коэффициентами.
Пример. Радиус R = 5 м; h = 1,5 м. Рассчитываем объем: V = 2 * π * R² * h / 3 = 2 * 3,14 * 5² * 1,5 / 3 = 78,5 м³.
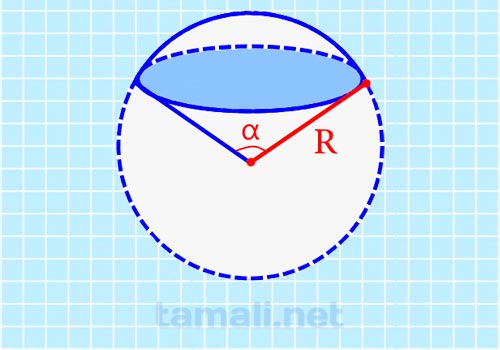
При известном радиусе шара и угла между осью и образующей конуса можно так же найти объем шарового сектора. Для это применяется формула:
где R – радиус шара, cos α – угол между осью и образующей конуса.
Пример. Вафельный рожок для мороженого, при заполнении мороженым имеющий форму шарового сектора, имеет такие размеры: радиус R = 11 см, угол α = 26°. Необходимо рассчитать объем мороженого в рожке при его заполнении. V = 2/3 * 3,14 * 11³ * (1 — cos 26º/2) = 71 см³.
Шаровой сектор – это геометрическое тело, возникающее при вращении сектора вокруг одного из его радиусов. Форму, близкую к шаровому сектору, имеют, в качестве примера, современные воздушные шары и мороженое в вафельном рожке.