Как найти объём прямого усечённого конуса зная радиусы оснований и высоту

Усеченным конус, или же коническим слоем принято называть геометрическую фигуру, которая находится в пространстве, то есть одна из частей конуса, которая осталась между основанием и секущей плоскостью, которая расположена параллельно с этим основанием. Усеченные конусы можно образовав при помощи вращения равнобедренной трапецией вокруг своей оси на 180 градусов, или прокрутив на 360 градусов прямоугольную трапецию вокруг боковой стороны, перпендикулярной основанию. Основными элементами усеченного конуса будут являться радиусы – большего\меньшего основания, и высота фигуры.

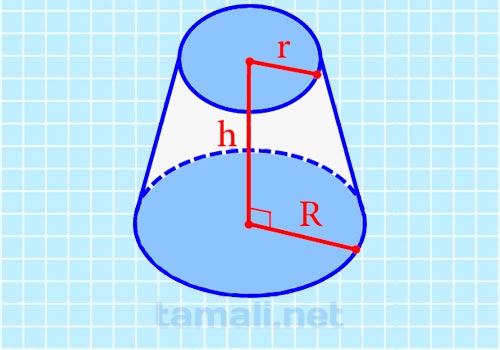
Для нахождения объема прямого усечённого конуса нужно воспользоваться данной выведенной формулой:

где R — радиус большего основания, r — радиус меньшого основания, h — высота, π — 3,14.

Пример. Дан некий конус, с высотой в 2 см, радиус меньшего основания также равен 2 см, большего – 3 см. От нас требуют определить объем фигуры. Это будет очень легко, если мы воспользуемся нашей формулой: V = (3,14 / 3) x 2(6 + 6 + 4) = 40 cм куб. Ответ: приблизительный объем фигура равен 40 см кубическим

На наглядном примере показано, что знание формулы поможет вам в решении любого сложного задания на нахождении объема усеченного конуса.