
Призма — это многогранник, который состоит из двух одинаковых многоугольников. Они расположены в разных плоскостях. Призмы различаются по количеству углов в основании. К примеру, если в основании находится треугольник ,то призма называется треугольной. Если в основании лежит четырехугольник, то рассматриваемая фигура четырехугольная. Таким образом, фигура, состоящая из 2 равносторонних треугольников, которые соединены между собой и лежат параллельно друг другу и называется правильная треугольная призма.
Чтобы было проще понять, рекомендуется начертить на листе бумаге объект 2 равных параллельных треугольника. Далее соединить их тремя вертикальными чертами. Все стороны у фигуры обозначаются латинскими буквами, например, «А» «B» «C». Для второго треугольника в призме буквы дублируются с индексом 1. В результате получается фигура, у которой стороны А₁В₁=В₁С₁=А₁С₁. Призма АBCА₁В₁С₁ имеет грани в виде параллелограммов. Сторона АА₁ называется боковым ребром. Стороны в основании геометрической фигуры называются ребрами основания. Высотой в призме называется расстояние между разными плоскостями.
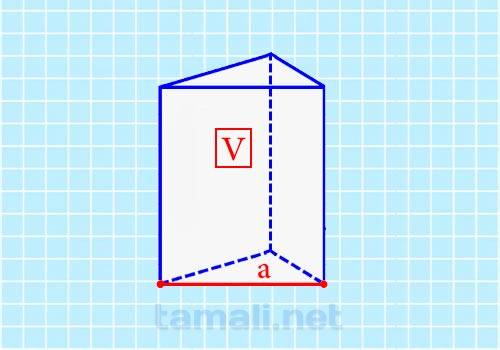
У этой фигуры есть два основания в виде треугольников. Шесть отрезков, которые образуют треугольник в призме и называют ребрами основания. Длина ребра в правильной призме будет одинаковой, поскольку все стороны и углы в равностороннем треугольнике равны между собой. Зная это и объем искомого многоугольника, можно применить эту формулу для осуществления расчетов:
где V — объем фигуры измеряется в кубических единицах, а — ребро основания.
Пример. Если V = 6 мм³, а = 6 мм то расчет неизвестной величины по формуле будет производиться следующим образом: H = 46 / 6²√3= 24 / 6² * 1.732 = 0,38 мм. Таким образом, применив формулу, можно узнать высоту через ребро основания и объем.
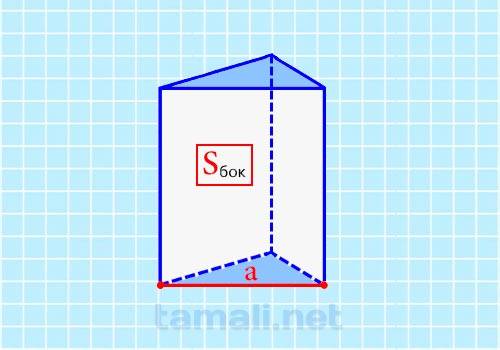
Для вычисления потребуется знать площадь боковой поверхности, а также ребро основания. Чтобы рассчитать площадь боковой поверхности, необходимо умножить периметр фигуры на длину бокового ребра. Она рассчитывается по данной формуле: Sбок = P * I, где P — периметр, I — длина бокового ребра. Зная площадь основания боковой поверхности и размеры отрезка, можно использовать формулу:
где Sбок — площадь боковой поверхности, а — ребро основания.
Пример. Для лучшего понимания можно продемонстрировать на конкретной задаче. Если = 7 мм², а = 8 мм то расчет неизвестной величины будет происходить следующим образом: H = 7 / 3 * 8 = 0,29 мм. Используя такой способ, можно узнать H правильной треугольной призмы.
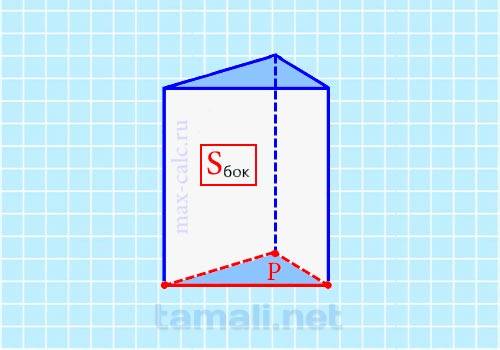
Под периметром равностороннего треугольника, который является основанием рассматриваемой фигуры, понимается сумма всех его длин, а также сторон. Зная, размер одной стороны легко рассчитать периметр. Найти площадь боковой поверхности можно по формуле рассмотренной выше. После того как периметр и боковая площадь известны, то необходимо подставить найденное значение в следующую формулу:
где S — площадь боковой поверхности, P — периметр основания.
Пример. Если P = 2 мм, а Sбок = 16 мм² то расчет размеров будет производиться следующим образом: H = 16 / 2 = 8 м². С помощью такого простого расчета можно вычислить H искомой фигуры.
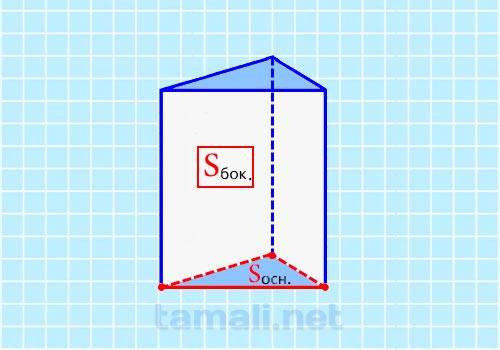
Площадь основания рассчитывается также, как при нахождении S равностороннего треугольника S = 1/2 * ah, но высота в этом случае неизвестна, поэтому придется воспользоваться другой формулой S = 1/2 * sin α. Как было сказано ранее, площадь боковой поверхности считается произведением периметра и длины бокового ребра. Найдя искомые площади, можно работать со следующей формулой для нахождения высоты призмы:
где Sбок — площадь боковой поверхности, Sосн — площадь основания геометрической фигуры.
Пример. Если Sбок = 10 мм², а Sосн = 15 мм² то расчет размеров проводится следующим образом: H = 10 / 3√4 * 15 / √3 = 0.5 мм. Таким образом, используя этот метод расчета, можно найти H.
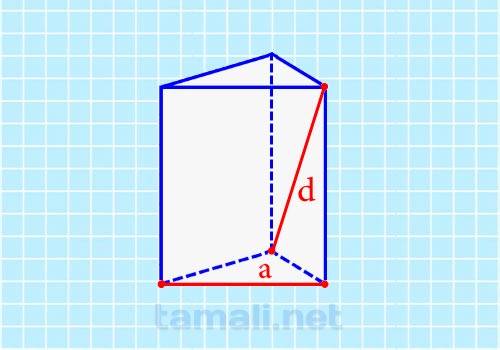
Под диагональю грани понимается луч, которые проходит между двумя вершинами, которые находятся на разных основаниях треугольной призмы. Когда известна диагональ грани, а также размер ребра в основании, можно решить задачу по этой формуле:
где d — диагональ грани, а — ребро основания.
Пример. Если d=9 мм², а = 5 мм то расчет искомого параметра по формуле будет выглядеть следующим образом: H = √(9² — 5²) = 7.4 мм. Таким образом, используя эту формулу, можно вычислить H.
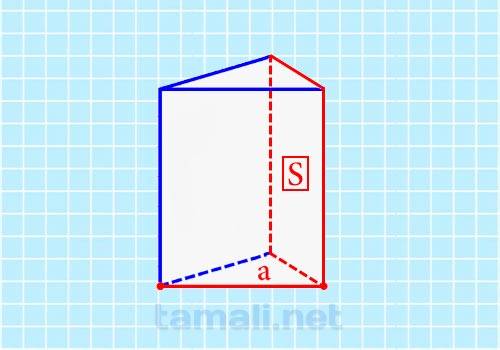
Ребро основания равняется длине любого отрезка в равностороннем треугольнике внутри призмы. Граней у призмы 3. Две боковые и одна задняя. Они изображены в виде параллелограммов. Зная длину и площадь грани у призмы, можно воспользоваться следующую формулу для расчета высоты правильной треугольной призмы:
где S — площадь грани, a — ребро основания.
Пример. Если S = 5 мм², а = 8 мм² то вычисления H будут производиться следующим способом: H = 5 / 8 = 0,62 мм. С помощью этой формулы можно найти искомую величину.
Умение рассчитать высоту треугольного многогранника пригодится при решении геометрических задач. Знания могут потребоваться в школе, в университете, но иногда такая необходимость может возникнуть в реальной жизни. Например, как строитель сможет посчитать площадь дома в виде призмы, если не знает расчетной формулы. Важно понимать, как найти неизвестные переменные, когда известно лишь несколько параметров.