На сегодняшний день существует несколько способов нахождения апофемы. Каждый из них стоит выбирать в зависимости от имеющихся в задаче данных.
Через высоту и ребро основания
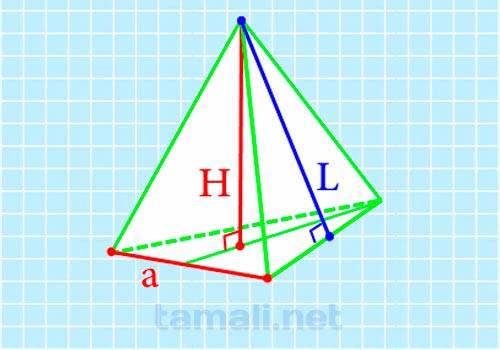
Первый способ включает в себя нахождение неизвестной через высоту пирамиды H и ребро основания a. Это возможно по следующей формуле:
где h — высота, a — ребро основания.
Кроме того стоит знать тригонометрические функции и их значения при различных углах. В данном случае тангенс 60º, который равен √3.
Пример. В задаче дана пирамида, у которой имеются два известных значения: высота равна 3, а сторона основания – 8. Требуется найти апофему правильной треугольной пирамиды. Тогда результат: b = √(3² + (8 / 2 tan60º)²)= √(9 + (4 / √3)²) = √(9 + (16 / 3)) = √(43/3) = 3.8
Через площадь боковых поверхностей и ребро нижнего основания
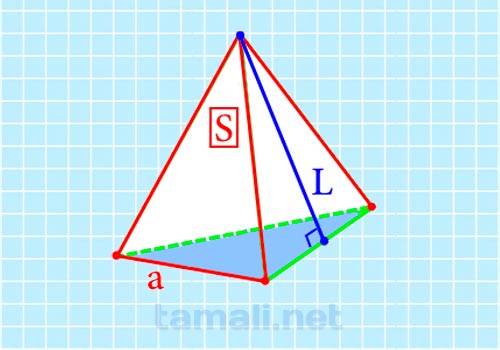
Второй вариант для нахождения вышеупомянутой неизвестной основан на площадях боковых поверхностей, которые являются треугольниками, и ребре основания a. Сначала стоит разобраться с площадью боковых поверхностей. Она состоит из суммы трех отдельных площадей боковых граней. Площадь прямоугольного треугольника: S = 0,5 * a * b, где а и b – это катеты прямоугольного треугольника. Площадь равностороннего треугольника: S = (a * a√3) / 4, где а – это ребро треугольника. Площадь произвольного треугольника: S = ah / 2, S = (a * b * sinα) / 2. Формула для нахождения апофемы правильной пирамиды через площадь боковых граней и ребро основания:
где Sбок — площадь боковых поверхностей, a — ребро основания.
Пример. Необходимо найти апофему правильной треугольной пирамиды, когда площадь боковых поверхностей равна 120, а ребро основания — 4. Решение: L = 120 / 3/2 * 4 = 20.
Через площадь боковых поверхностей и периметр нижнего основания
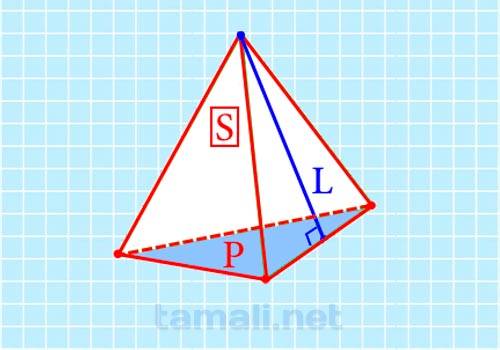
Есть еще и третий способ, который основан на площади боковых поверхностей и периметре основания. Периметр основания — это сумма длин всех сторон, который принадлежат основанию. В правильном треугольнике длину одного ребра умножают на три. Формула:
где Sбок — площадь боковых поверхностей, P — периметр основания.
Пример. Необходимо найти апофему правильной треугольной пирамиды, когда площадь боковых поверхностей равна 120, а периметр — 12. Решение: апофема равна L = 120 / 1/2 * 12 = 120 * 6 = 20.
Пирамида представляет собой объемную геометрическую фигуру, многогранник, в основании которого лежит n-угольник, а остальные n граней- треугольники с общей вершиной, называющейся вершиной пирамиды. Правильная пирамида – это пирамида, в основании которой лежит правильный многоугольник, а боковые ребра равны. У треугольной пирамиды за основание принимают треугольник.
Апофемой принято называть высоту боковой грани. Это перпендикуляр, который был опущен из вершины грани на противолежащую сторону. Часто её обозначают латинской буквой L или же h, но обязательно маленькой, потому что большая – это высота не грани, а самой пирамиды. Все апофемы правильной треугольной пирамиды будут равны между собой. Апофема правильной треугольной пирамиды равна отношению площади боковых поверхностей на половину периметра нижнего основания.
