Найти высоту правильной треугольной пирамиды онлайн

Правильная треугольная пирамида – это пирамида, у которой в основании лежит правильный, иными словами, равносторонний треугольник и у которой боковые стороны – это равнобедренные треугольники. Такая объемная фигура также именуется правильным тетраэдром. Высота – это отрезок перпендикуляра, проведенного из вершины фигуры на основание или на продолжение основания. Обозначается латинской буквой h и на чертеже отмечается квадратом. Высота треугольной пирамиды, проведенная из вершины, попадает на основание в центр пересечения медиан фигуры.

Через объём и площадь основания

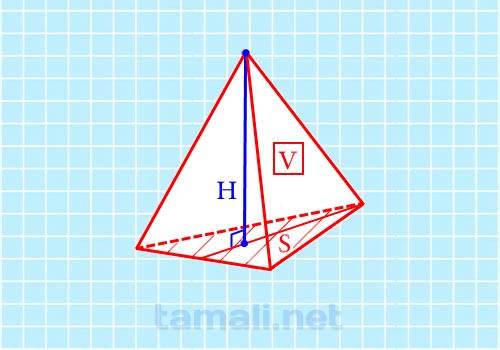
Объем любой пирамиды находится по формуле: V = 1/3h * S, где h является высотой пирамиды, а S является площадью основания пирамиды. Из этой формулы можно получить формулу для нахождения высоты пирамиды:

Пример. По условию дана правильная треугольная пирамида, у которой площадь основания равна S = 18 см², а объем равен V = 90 смᶾ, нужно найти высоту фигуру. Для этого нужно подставить в формулу все известны переменные, тогда h = 90 * 3 / 18 = 15, значит высота равна 15 см. Так можно находить высоту и правильной, и наклонной фигуры.

Через объём и ребро основания

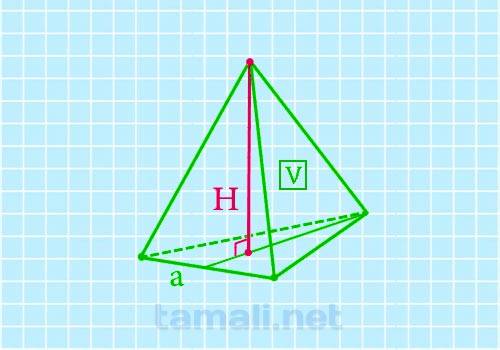
Найти высоту правильной треугольной пирамиды можно также через объем и ребро основания в случае, когда неизвестна площадь основания. Вычисления в данном случае надо производить по формуле:

Пример. Дана правильная треугольная пирамида с объемом V = 90 смᶾ и длиной ребра основания a = 5 см, нужно найти высоту этой фигуры. Подставим значения в формулу и получим:  H = √ (90 * 4 * √3 / 5²) = 5 см.

Найти высоту правильной треугольной пирамиды можно также через объем и ребро основания по-другому. Итак, V = 1/3h * S, значит h = V * 3 / S. Поскольку площадь основания нам не известна, но известно ребро, то площадь можно выразить по формуле: S = 1/2 * a * b * sin α, где a и b равны между собой, поскольку пирамида по условию задачи является правильной, а sin α = sin 60°, в равностороннем треугольнике все углы раны 60°.

Подставив формулу площади основания пирамиды через стороны треугольника и синус в исходную формулу, получим: h = (V * 3 * 2) / (a * b * sin α).

Пример. Дана правильная треугольная пирамида с объемом V = 90 смᶾ и длиной ребра основания a = 5 см, нужно найти высоту этой фигуры. При решении задачи сначала необходимо выполнить все преобразования, описанные выше, а затем уже переходить к подстановке числовых значений. Это принцип соблюдения логики при решении математических задач. В ином случае вам не поставят полный балл за задачу, поскольку конечной формулы нет в кодификаторе. Выполнив все преобразования можно подставлять числа, получается: h = (90 * 3 * 2) / (5 * 5 * (√3 / 2)), преобразовываем это выражение до h = (18 * 3 * 2 * 2) / (5 * √3), получается h = (72 * 3 * √3) / (5 * 3) = (72 * √3) / 5.

Получается для того, чтобы вычислить высоту в правильной треугольной пирамиде (тетраэдре) прежде всего так или иначе нужно отыскать площадь основания и объем фигуры. Чтобы определить площадь достаточно иметь данные об одном из ребер основания фигуры. Вычисление высоты пирамиды может пригодиться при нахождении объема фигуры.