
Пирамидой в стереометрии называется объёмная фигура, образуемая многоугольником и расположенной вне его плоскости точкой. Эта точка соединена с точками в вершинах многоугольника отрезками, которые называются рёбрами пирамиды. Сам многоугольник — это основание пирамиды. При треугольном основании пирамида будет носить название треугольной, при четырёхугольном – четырёхугольной, и так далее.
Приведём варианты вычисления апофемы правильной четырёхугольной пирамиды в зависимости от исходных
данных пространственной фигуры. Заданная пирамида обозначена SABCD, где S – вершина, а ABCD –
вершины квадрата в основании.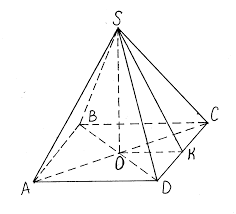
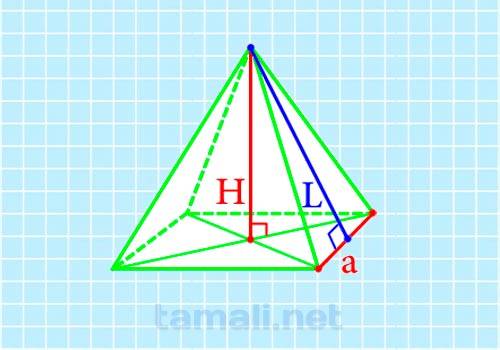
Апофема пирамиды при известных значениях её высоты SO и стороны квадрата в основании AD=DC=BC=AB вычисляется по формуле гипотенузы для прямоугольного треугольника SOK. В этом треугольнике одним из катетов будет высота SO, вторым – половинное значение заданной стороны основания OK=1/2 AD. Значит: SK²= OK²+ SO² или SK= (1/2 AD) ²+ SO²) или
где H — высота, a — ребро основания.
Пример. Пусть высота SO = 4, а сторона основания AD = 6. Тогда апофема L находится следующим образом: L = √ (( 6 / 2)² + 4²) = 5
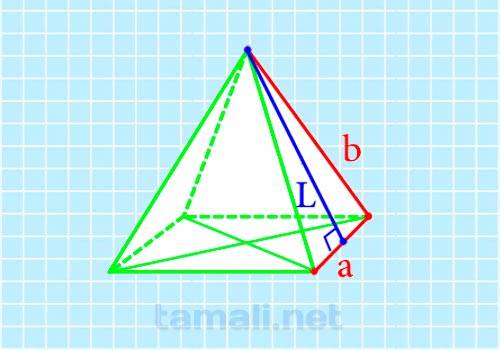
При известном значении бокового ребра SD и стороны основания CD для нахождения апофемы SK также используется теорема Пифагора. В этом случае рассматривается прямоугольный треугольник SKD, гипотенузой которого выступает боковое ребро SD, одним из катетов – отрезок стороны основания DK, а вторым – апофема SK. Первый катет равен половине стороны квадрата в основании, поскольку апофема равнобедренного треугольника, коим является боковая грань пирамиды, является для него и медианой, делящей основание пополам: DK = 1/2 DC. Отсюда следует, что SD²= DK²+ SK², а SK²= SD²- DK² или, подставляя, получаем выражение: SK² = SD² — (1/2 DC)², откуда SK = √(SD² — (1/2 DC )²) или
где a — ребро основания, b — боковое ребро.
Пример. Пусть боковое ребро SD равно 5, а сторона основания – 6. Тогда, подставляя указанные числовые значения, вычисляем значение апофемы: SK =5² – (6 / 2)² ) = 4.
Апофема при известной суммарной площади боковых поверхностей Sбок и значении ребра основания CD вычисляется по следующей схеме. Вначале следует определить площадь каждой из четырёх граней, что легко сделать, зная, что все они для правильной пирамиды равны между собой. Поэтому общая площадь делится на четыре равные части: Ssdc = Sбок /4. Затем, при известном значении площади боковой грани и ребра основания, по формуле площади равнобедренного треугольника находится его высота, то есть искомая апофема: Ssdc = ½ SK * CD откуда SK = 2Ssdc / CD. Или, подставляя выведенную площадь грани, SK = 2(Sбок /4) / CD. Преобразив, получаем: SK = Sбок /2CD или
где Sбок — площадь боковых поверхностей, a — ребро основания.
Пример. Допустим, в задаче задана общая площадь боковой поверхности правильной четырёхугольной пирамиды Sбок = 48 и ребро основания CD = 6. Найдём, используя выведенную формулу, значение апофемы: SK = 48 / 2 * 6 = 4.
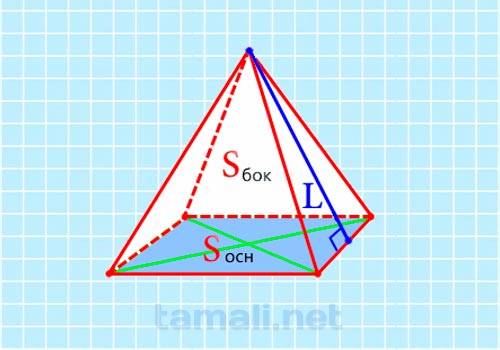
Апофема при известных значениях суммарной площади боковых поверхностей Sбок и площади основания Sосн вычисляется следующим образом. В первую очередь следует найти ребро основания. Площадь основания пирамиды – квадрата – является произведением двух его сторон либо квадратом стороны. Значит, значение стороны основания вычисляем по формуле Sосн = CD² или CD = √Sосн. Теперь, зная суммарную площадь боковой поверхности четырёхугольной пирамиды, делением на 4 находим площадь боковой грани – равнобедренного треугольника SCD: Ssdc = Sбок / 4. Его площадь также вычисляется, как произведение основания на высоту, делённое на два: Ssdc =½CD * SK или Sбок/4 =½CD * SK отсюда SK = 2 (Sбок / 4) / CD или, сократив и подставив выражение для CD: SK = Sбок / 2 Sосн, где SK – высота грани и искомая апофема.
где Sбок — площадь боковых поверхностей, Sосн — площадь основания.
Пример. Возьмём для примера численные значения, Sбок = 48 и Sосн = 36. Подставляя, получаем результат: SK = 48 / (2 * √36) = 4.
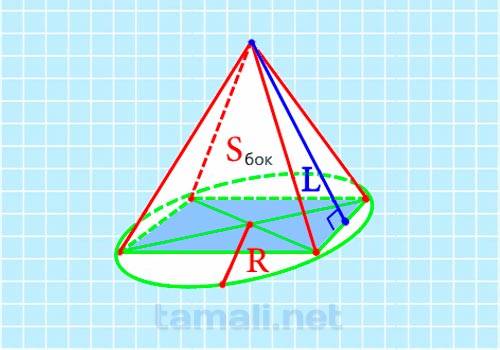
Найдём апофему при известной площади боковых поверхностей Sбок и радиусе R описанной вокруг основания ABCD окружности. Рассмотрим прямоугольный треугольник COD, образованный половинами диагоналей этого квадрата CO и OD, равными заданному радиусу, и гранью в основании CD. Эта сторона в данном треугольнике выступает гипотенузой. Её можно вывести из теоремы Пифагора: CD² = OD² + OC², откуда CD = √(OD²+OC²) или CD = √2R²= R√2. Теперь определим площадь каждой боковой грани. Она находится путём деления площади полной боковой поверхности пирамиды на 4: Ssdc = Sбок / 4. По формуле, связывающей площадь равнобедренного треугольника SDC с его высотой и основанием, выделяем высоту-апофему: Ssdc =½CD * SK Или, подставляя выведенное выше выражение: Sбок/4 = ½CD * SK. Далее преобразовываем для выделения SK: SK=(2 Sбок/4) / CD или, подставляя выведенное для CD выражение и сокращая, получаем: SK= Sбок / 2R * √2.
где Sбок — площадь боковых поверхностей, R — радиус описанной окружности.
Пример. Подставляя для примера числовые значения R = 3√2 и Sбок = 48, получаем в результате значение апофемы: SK=48 / 2 * (3√2 * √2)=4.
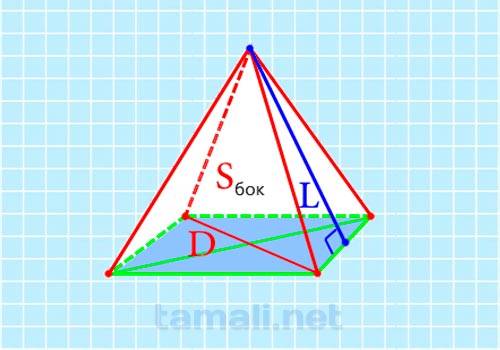
Поскольку стороны квадрата ABCD в основании равны и угол между смежными сторонами прямой, значения этих сторон можно найти, рассматривая прямоугольный треугольник ADC, где заданная диагональ AC является гипотенузой, а неизвестные стороны AD и CD – равными катетами. Вычисляем их значения по теореме Пифагора: AC² = AD² + CD² = 2CD² откуда CD = √(AC² / 2) = AC / √2. Найденное значение стороны основания позволяет найти апофему — высоту боковой грани SK — при известной площади этой грани. Суммарная площадь боковой поверхности заданной фигуры Sбок даёт возможность найти площадь каждой её боковой плоскости. То есть Sscd = Sбок / 4. А теперь Sscd иначе выразим через высоту и основание грани: Sscd = 1/2 * (SK * CD) или, подставляя ранее выведенную формулу для CD: Sscd = 1/2 * (SK * ( AC / √2). Теперь все данные кроме искомой апофемы SK у нас присутствуют, поэтому преобразуем выражение, заменяя SSCD и сокращая: SK= 2 * √2 * Sscd / AC = 2 * √2 (Sбок / 4) / AC = Sбок * √2 / 2АС.
где Sбок — площадь боковых поверхностей, D — диагональ основания.
Пример. Допустим, диагональ в основании равна 6√2, а суммарная площадь боковых граней – 48. Тогда, подставляя числовые значения в полученное выше выражение, вычисляем: SK = 48√2 / 2 * (6√2) = 4
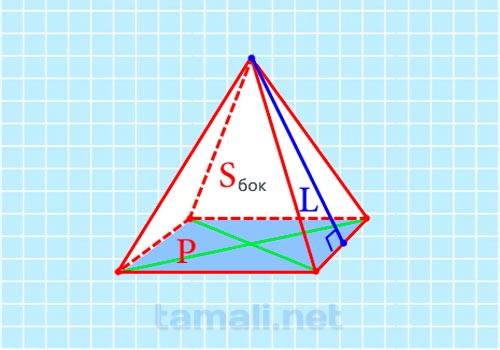
Исходными данными, на которые можно опереться при вычислении апофемы для этой задачи, являются Sбок и Росн. Известное значение периметра квадрата ABCD в основании пирамиды Росн даёт возможность найти значение его сторон, которые равны между собой как стороны квадрата и находятся путём деления периметра на 4 равные части: AB = BC = CD = AD = Рabcd / 4. Теперь ребро CD, одновременно являясь основанием боковой грани SCD, позволяет вычислить её высоту SK – искомую апофему, при известном значении боковой площади пирамиды. Площадь каждой из 4-х граней найдём путём деления общей площади на равные части: Sscd= Sбок/4. Далее из формулы площади равнобедренного треугольника SCD через высоту и основание найдём апофему SK. Sscd = 1/2 * (SK * CD) или SK = 2* Sscd / CD. Подставляя выведенные выше через общую площадь и периметр основания значения площади грани и ребро её основания соответственно, получаем: SK = 2 * (Sбок / 4) / (Рabcd / 4). Или SK = 2Sбок / Рabcd
где Sбок — площадь боковых поверхностей, P — периметр основания.
Пример. Предположим, что площадь боковой поверхности Sбок равно 48, периметр основания – 24. Подставляя данные числовые значения, получаем следующий результат: SK= 2 * (48 / 4) / (24 / 4) = 4.
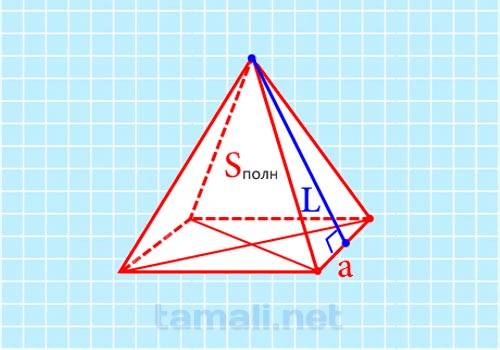
Полная площадь поверхности Sполн в этом случае представляет собой сумму полной площади боковой поверхности Sбок фигуры и площади квадрата в её основании – Sabcd, сторона которого CD задана условием задачи. Апофему удобнее всего найти через площадь боковой грани, имея значение её основания: Sscd = 1/2 * (SK * CD). Преобразуя формулу, получаем: SK = 2* Sscd / CD. Вычтя из площади полной поверхности пирамиды площадь основания, которую можно найти при его заданном ребре, получаем полную площадь боковой поверхности: Sполн= Sбок + Sabcd, откуда Sбок= Sполн — Sabcd. Здесь площадь квадрата в основании легко найти, зная его ребро: Sabcd = CD² и тогда, подставляя: Sбок = Sполн — CD². Разделив Sбок на 4 равные части, получим площадь боковой грани: Sбок / 4 = (Sполн- CD²) / 4= Sscd. Теперь, подставив в формулу для вычисления высоты боковой грани найденное выражение, получим: SK = 2* ((Sполн — CD²) /4) / CD или, выполнив сокращение: SK = (Sполн — CD²) /2CD.
где Sполн — площадь полной поверхности, a — ребро основания.
Пример. Допустим, нам задана общая площадь фигуры S = 84, а ребро её основания – CD
= 6. Тогда, подставляя значения в полученное выражение, находим:
SK = (84 — 62) / (2 * 6) = 4.
Правильной пирамидой называется такая фигура, в основании которой лежит многоугольник с равными сторонами, то есть правильный. При этом проекция вершины на его плоскость является центром вписанной в это многоугольное основание и описанной вокруг него окружностей. Отличительными признаками правильной четырёхугольной пирамиды являются квадрат в основании и лежащая в точке пересечения его диагоналей проекция вершины на этот квадрат.
Боковые плоскости (грани) правильной пирамиды – равнобедренные треугольники. Основание каждого из них
одновременно является и стороной основания пирамиды.
Проведенная к основанию высота боковых
граней, имеющая для каждой из них одинаковое значение, называется апофемой. Это понятие применяется
при решении множества геометрических задач, в которых фигурирует правильная пирамида с квадратом в
основании. В зависимости от других исходных данных, апофема даёт возможность вычислить площадь
боковой поверхности фигуры, её высоту, длину ребер и сторону основания.