
Правильная четырёхугольная пирамида – это пространственная фигура, образуемая пятью плоскостями, которые называются гранями. Четыре из них – треугольные фигуры с имеющими одинаковую длину боковыми сторонами (равнобедренные). Эти треугольные грани вместе называют боковой поверхностью фигуры. Они опираются своими основаниями на равносторонний прямоугольник (квадрат). Этот квадрат – пятая грань объёмного объекта — есть её основание. Четыре боковые плоскости четырёхугольной пирамиды, являющейся правильной — это треугольники с двумя равными боковыми сторонами. То есть равнобедренные. Эти стороны являются общими для соседних боковых граней.
Точка, в которой сходятся боковые стороны этих четырёх граней, является вершиной пирамиды, а проекция этой точки совпадает с точкой пересечения соединяющих противоположные углы основания диагоналей. Этот отрезок, соединяющий вершину фигуры с её проекцией на квадратное основание, выступает высотой пирамиды и используется во многих формулах для вычисления параметров пространственной фигуры.
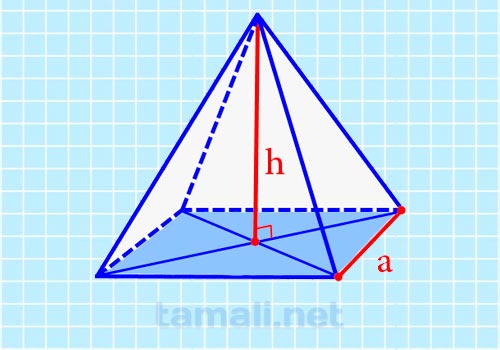
Выражение, дающее возможность найти объём V пирамиды при известных значениях ребра основания фигуры – a, и её высоты — h, выглядит так:
где a — ребро основания, h — высота.
Здесь квадрат стороны основания представляет собой его площадь, поэтому данную формулу можно запомнить и как треть произведения высоты фигуры на площадь её основания.
Пример. Пусть для примера у заданной правильной четырёхугольной пирамиды ребро основания a = 10 см, а высота h = 15 см. Подставив в формулу эти значения, получаем: V = 1/3 * (15 * 10²)=500 см².